Содержание
Сколько штук досок в 1 кубе: таблица и пример расчета
Главная | Статьи | Сколько досок в 1 кубе
Для упрощения счета, мы подготовили для Вас сводную таблицу. Таблица позволяет сразу узнать, сколько досок в 1 кубе, не уделяя время расчетам. Чтобы Вам было удобно.
Сколько штук обрезной и строганной доски в 1 кубе таблица
| Размеры, мм | Объём досок в 1 м3 | Количество досок в м3 | Количество досок в м2 |
| 20х100х6000 | 0,012 м3 | 83 шт. | 50 м2 |
| 20х120х6000 | 0,0144 м3 | 69 шт. | 50 м2 |
| 20х150х6000 | 0,018 м3 | 55 шт. | 50 м2 |
| 20х180х6000 | 0,0216 м3 | 46 шт. | 50 м2 |
| 20х200х6000 | 0,024 м3 | 41 шт. | 50 м2 |
| 20х250х6000 | 0,03 м3 | 33 шт. | 50 м2 |
| 25х100х6000 | 0,015 м3 | 67 шт. | 40 м2 |
| 25х120х6000 | 0,018 м3 | 55 шт. | 40 м2 |
| 25х150х6000 | 0,0225 м3 | 44 шт. | 40 м2 |
| 25х180х6000 | 0,027 м3 | 37 шт. | 40 м2 |
| 25х200х6000 | 0,03 м3 | 33 шт. | 40 м2 |
| 25х250х6000 | 0,0375 м3 | 26 шт. | 40 м2 |
| 30х100х6000 | 0,018 м3 | 55 шт. | 33 м2 |
| 30х120х6000 | 0,0216 м3 | 46 шт. | 33 м2 |
| 30х150х6000 | 0,027 м3 | 37 шт. | 33 м2 |
| 30х180х6000 | 0,0324 м3 | 30 шт. | 33 м2 |
| 30х200х6000 | 0,036 м3 | 27 шт. | 33 м2 |
| 30х250х6000 | 0,045 м3 | 22 шт. | 33 м2 |
| 32х100х6000 | 0,0192 м3 | 52 шт. | 31 м2 |
| 32х120х6000 | 0,023 м3 | 43 шт. | 31 м2 |
| 32х150х6000 | 0,0288 м3 | 34 шт. | 31 м2 |
| 32х180х6000 | 0,0346 м³ | 28 шт. | 31 м2 |
| 32х200х6000 | 0,0384 м3 | 26 шт. | 31 м2 |
| 32х250х6000 | 0,048 м3 | 20 шт. | 31 м2 |
| 40х100х6000 | 0,024 м3 | 41 шт. | 25 м2 |
| 40х120х6000 | 0,0288 м3 | 34 шт. | 25 м2 |
| 40х150х6000 | 0,036 м3 | 27 шт. | 25 м2 |
| 40х180х6000 | 0,0432 м3 | 23 шт. | 25 м2 |
| 40х200х6000 | 0,048 м3 | 20 шт. | 25 м2 |
| 40х250х6000 | 0,06 м3 | 16 шт. | 25 м2 |
| 50х100х6000 | 0,03 м3 | 33 шт. | 20 м2 |
| 50х120х6000 | 0,036 м3 | 27 шт.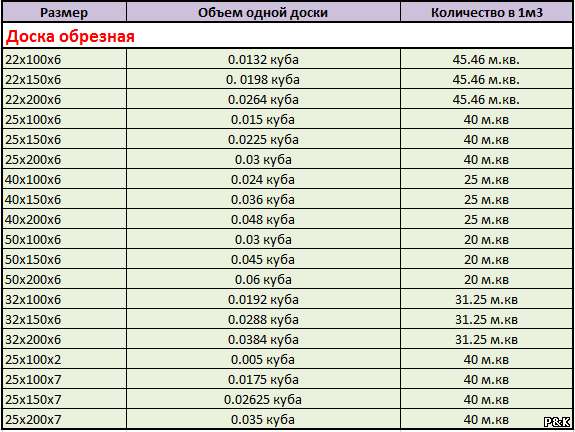 | 20 м2 |
| 50х150х6000 | 0,045 м3 | 22 шт. | 20 м2 |
| 50х180х6000 | 0,054 м3 | 18 шт. | 20 м2 |
| 50х200х6000 | 0,06 м3 | 16 шт. | 20 м2 |
| 50х250х6000 | 0,075 м3 | 13 шт. | 20 м2 |
Формулы расчета доски
Примеры расчета доски размером 20х100х6000 мм
Формула расчета объема доски:
0,02 м · 0,1 м · 6 м = 0,012 м3
Формула расчета доски в кубе в штуках:
1 м3 / 0,012 м3 = 83 шт./м3
Формула расчета доски в кубе в квадратах:
1 м3 / 0,02 м = 50 м2/м3
Чтобы решить, сколько досок в 1 кубе, сначала нужно знать основные параметры приобретаемого материала – толщину, ширину и длину. Также можно делать расчет для досок размером 3 метра, 4 метра, 5 метров.
Также можно делать расчет для досок размером 3 метра, 4 метра, 5 метров.
Страница содержит ответы на простые вопросы людей:
- Сколько досок
- Сколько кубов доски
- Сколько штук досок
- Досок в кубе
- Сколько кубов в досках
- Сколько штук в одном кубе
- Сколько в кубе обрезной доски
- Как подсчитать сколько досок в 1 кубе
Зачем считать, сколько досок в 1 кубе?
Всего две причины для того, чтобы произвести расчеты:
- Вы узнаете общую цену всего объема бруса, нужного для вашего проекта. Достаточно знать цену за 1 доску и сколько всего штук (определяется расчетным путем или из нашей таблицы для стандартных размеров досок).
- Вы подсчитаете общее число досок, нужное для осуществления вашего проекта. И сделать расчет можно, зная, сколько нужно кубов материала для работы, и определив количество штук досок в 1 кубе.
Но если боитесь сделать неправильные расчеты, позвоните по телефонам +7 (495) 775-83-74 или 8 (800) 775-83-74 и наши специалисты помогут разобраться с правильным подсчетом!
таблица 3 и 6 метров
Чтобы узнать количество разных по длине досок в 1 кубе, можно применить таблицу или провести расчёт самостоятельно.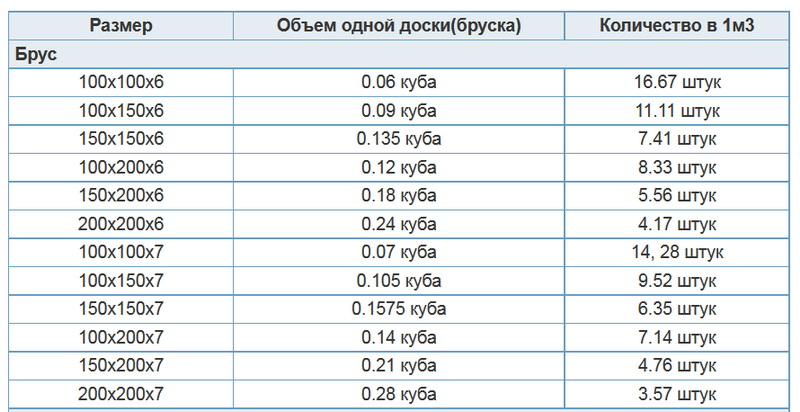 Реализация продукции происходит в кубических метрах, при этом указывают следующие параметры:
Реализация продукции происходит в кубических метрах, при этом указывают следующие параметры:
- Длина — метр или миллиметр.
- Ширина и толщина — миллиметр.
Все единицы измерения переводим в метры.
Расчёт: 1 м3, разделить на объём доски, он будет — 0,045 м3, получим — 22,2 шт.
Получилось не целое число, но при покупке объём будет соблюдаться. Для реализации предлагается пиломатериал больше по длине, на несколько сантиметров. Чтобы не возникло недостатка, который может получиться за счёт ширины поперечного распила.
Ниже представлена таблица, из которой видно, сколько досок в 1 кубе по 6 метров.
| Размер сечения, мм | Длина, м | Количество досок в 1 кубе |
| 25х100 | 6 | 66,67 |
| 25х150 | 6 | 44,44 |
| 40х100 | 6 | 41,67 |
| 50х100 | 6 | 33,33 |
| 40х150 | 6 | 27,78 |
| 50х150 | 6 | 22,22 |
| 50х200 | 6 | 16,67 |
Если нужны доски диной 3 метра одинаковой толщины, то количество следует умножить на два.
Ниже представлена таблица, из которой видно, сколько досок в 1 кубе по 3 метра.
| Размер сечения, мм | Длина, м | Количество досок в 1 кубе |
| 25х100 | 3 | 133,34 |
| 25х150 | 3 | 88,88 |
| 40х100 | 3 | 83,34 |
| 50х100 | 3 | 66,66 |
| 40х150 | 3 | 55,56 |
| 50х150 | 3 | 44,44 |
| 50х200 | 3 | 33,34 |
колько досок в кубе. Количество досок в одном кубическом метре
Сколько досок в кубе?
Количество штук доски в одном кубе зависит от размеров доски .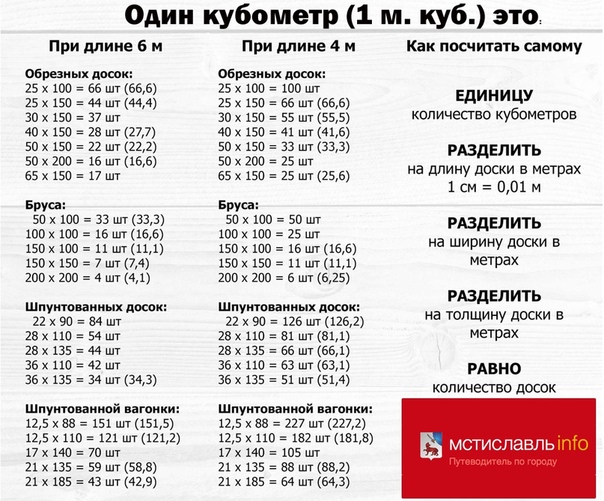 Необходимое количество обрезных досок и сколько квадратных метров покрывает 1 кубический метр доски, можно посчитать, используя таблицы пилорамы “78 Досок”.
Необходимое количество обрезных досок и сколько квадратных метров покрывает 1 кубический метр доски, можно посчитать, используя таблицы пилорамы “78 Досок”.
Каталог пиломатериалов и цены на них можно посмотреть по этой ссылке.
Сколько 6-ти метровых досок в 1 кубе: таблица
| Размеры доски, мм | Количество в 1 кубе | Площадь, покрываемая 1 м3 доски |
|---|---|---|
| Сколько досок толщиной 20мм в кубе («двадцатка») | ||
| 20×100×6000 | 83 шт. | 49,8 м2 |
| 20×120×6000 | 69 шт. | 49,7 м2 |
| 20×150×6000 | 55 шт. | 49,5 м2 |
| 20×180×6000 | 46 шт. | 49,7 м2 |
| 20×200×6000 | 41 шт. | 49,2 м2 |
| 20×250×6000 | 33 шт. | 49,5 м2 |
| Сколько досок толщиной 25 мм в кубе («двадцатьпятка») | ||
| 25×100×6000 | 66 шт. | 39,6 м2 |
| 25×120×6000 | 55 шт. | 39,6 м2 |
| 25×150×6000 | 44 шт. | 39,6 м2 |
| 25×180×6000 | 37 шт. | 40 м2 |
| 25×200×6000 | 33 шт. | 39,6 м2 |
| 25×250×6000 | 26 шт. | 39 м2 |
| Сколько досок толщиной 30 мм в кубе («тридцатка») | ||
| 30×100×6000 | 55 шт. | 33 м2 |
| 30×120×6000 | 46 шт. | 33,1 м2 |
| 30×150×6000 | 37 шт. | 33,3 м2 |
| 30×180×6000 | 30 шт. | 32,4 м2 |
| 30×200×6000 | 27 шт. | 32,4 м2 |
| 30×250×6000 | 22 шт. | 33 м2 |
| Сколько досок толщиной 32 мм в кубе («тридцатидвушка») | ||
| 32×100×6000 | 52 шт. | 31,2 м2 |
| 32×120×6000 | 43 шт. | 31 м2 |
| 32×150×6000 | 34 шт. | 30,6 м2 |
| 32×180×6000 | 28 шт. | 30,2 м2 |
| 32×200×6000 | 26 шт. | 31,2 м2 |
| 32×250×6000 | 20 шт. | 30 м2 |
| Сколько досок толщиной 40 мм в кубе («сороковка») | ||
| 40×100×6000 | 41 шт. | 24,6 м2 |
| 40×120×6000 | 34 шт. | 24,5 м2 |
| 40×150×6000 | 27 шт. | 24,3 м2 |
| 40×180×6000 | 23 шт. | 24,8 м2 |
| 40×200×6000 | 20 шт. | 24 м2 |
| 40×250×6000 | 16 шт. | 24 м2 |
| Сколько досок толщиной 40 мм в кубе («пятидесятка») | ||
| 50×100×6000 | 33 шт. | 19,8 м2 |
| 50×120×6000 | 27 шт. | 19,4 м2 |
| 50×150×6000 | 22 шт. | 19,8 м2 |
| 50×180×6000 | 18 шт. | 19,4 м2 |
| 50×200×6000 | 16 шт. | 19,2 м2 |
| 50×250×6000 | 13 шт. | 19,5 м2 |
Сколько 4-х метровых досок в 1 кубе: таблица
| Размеры доски, мм | Количество в 1 кубе | Площадь, покрываемая 1 м3 доски |
|---|---|---|
| Доска-«двадцатка» (толщина 20 мм) | ||
| 20×100×4000 | 125 шт. | 50 м2 |
| 20×120×4000 | 104 шт. | 49,9 м2 |
| 20×150×4000 | 83 шт. | 49,8 м2 |
| 20×180×4000 | 69 шт. | 49,7 м2 |
| 20×200×4000 | 62 шт. | 49,6 м2 |
| 20×250×4000 | 50 шт. | 50 м2 |
| Доска-«двадцатьпятка» (толщина 25 мм) | ||
| 25×100×4000 | 100 шт. | 40 м2 |
| 25×120×4000 | 83 шт. | 39,8 м2 |
| 25×150×4000 | 66 шт. | 39,6 м2 |
| 25×180×4000 | 55 шт. | 39,6 м2 |
| 25×200×4000 | 50 шт. | 40 м2 |
| 25×250×4000 | 40 шт. | 40 м2 |
| Доска-«тридцатка» (толщина 30 мм) | ||
| 30×100×4000 | 83 шт. | 33,2 м2 |
| 30×120×4000 | 69 шт. | 33,1 м2 |
| 30×150×4000 | 55 шт. | 33 м2 |
| 30×180×4000 | 46 шт. | 33,1 м2 |
| 30×200×4000 | 41 шт.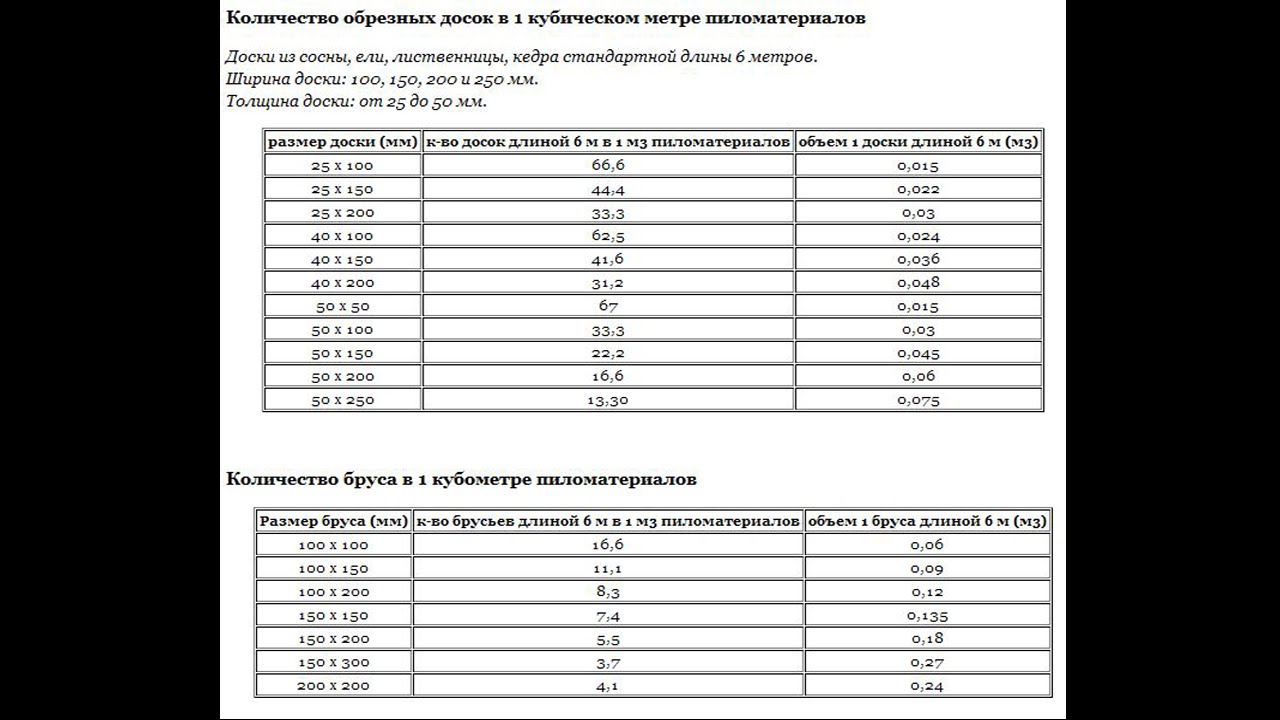 | 32,8 м2 |
| 30×250×4000 | 33 шт. | 33 м2 |
| Доска-«тридцатидвушка» (толщина 32 мм) | ||
| 32×100×4000 | 78 шт. | 31,2 м2 |
| 32×120×4000 | 65 шт. | 31,2 м2 |
| 32×150×4000 | 52 шт. | 31,2 м2 |
| 32×180×4000 | 43 шт. | 31 м2 |
| 32×200×4000 | 39 шт. | 31,2 м2 |
| 32×250×4000 | 31 шт. | 31 м2 |
| Доска-«сороковка» (толщина 40 мм) | ||
| 40×100×4000 | 62 шт. | 24,8 м2 |
| 40×120×4000 | 52 шт. | 25 м2 |
| 40×150×4000 | 41 шт. | 24,6 м2 |
| 40×180×4000 | 34 шт. | 24,5 м2 |
| 40×200×4000 | 31 шт. | 24,8 м2 |
| 40×250×4000 | 25 шт. | 25 м2 |
| Доска-«пятидесятка» (толщина 50 мм) | ||
| 50×100×4000 | 50 шт. | 20 м2 |
| 50×120×4000 | 41 шт. | 19,7 м2 |
| 50×150×4000 | 33 шт. | 19,8 м2 |
| 50×180×4000 | 27 шт. | 19,4 м2 |
| 50×200×4000 | 25 шт. | 20 м2 |
| 50×250×4000 | 20 шт. | 20 м2 |
Узнать цены на пиломатериалы нашей пилорамы “78 Досок” в Яльгелево с доставкой по Санкт-Петербурге с Ленинградской области можно в разделе “ЦЕНЫ“
Как заказать?
Сделать заказ можно по телефону: +7(812)984-78-78
[table id=dostavka /]
| Пиломатериал | Размер | Объем 1-й штуки | Штук в 1 м³ | м² в 1 м³ |
|---|---|---|---|---|
| Доска обрезная | 20×100×6000 | 0,012 м³ | 83 шт. | 50 м² |
| Доска обрезная | 20×120×6000 | 0,0144 м³ | 69 шт. | 50 м² |
| Доска обрезная | 20×150×6000 | 0,018 м³ | 55 шт. | 50 м² |
| Доска обрезная | 20×180×6000 | 0,0216 м³ | 46 шт. | 50 м² |
| Доска обрезная | 20×200×6000 | 0,024 м³ | 41 шт. | 50 м² |
| Доска обрезная | 20×250×6000 | 0,03 м³ | 33 шт. | 50 м² |
| Доска обрезная | 25×100×6000 | 0,015 м³ | 67 шт. | 40 м² |
| Доска обрезная | 25×120×6000 | 0,018 м³ | 55 шт. | 40 м² |
| Доска обрезная | 25×150×6000 | 0,0225 м³ | 44 шт. | 40 м² |
| Доска обрезная | 25×180×6000 | 0,027 м³ | 37 шт. | 40 м² |
| Доска обрезная | 25×200×6000 | 0,03 м³ | 33 шт. | 40 м² |
| Доска обрезная | 25×250×6000 | 0,0375 м³ | 26 шт. | 40 м² |
| Доска обрезная | 30×100×6000 | 0,018 м³ | 55 шт. | 33 м² |
| Доска обрезная | 30×120×6000 | 0,0216 м³ | 46 шт. | 33 м² |
| Доска обрезная | 30×150×6000 | 0,027 м³ | 37 шт. | 33 м² |
| Доска обрезная | 30×180×6000 | 0,0324 м³ | 30 шт. | 33 м² |
| Доска обрезная | 30×200×6000 | 0,036 м³ | 27 шт. | 33 м² |
| Доска обрезная | 30×250×6000 | 0,045 м³ | 22 шт. | 33 м² |
| Доска обрезная | 32×100×6000 | 0,0192 м³ | 52 шт. | 31 м² |
| Доска обрезная | 32×120×6000 | 0,023 м³ | 43 шт. | 31 м² |
| Доска обрезная | 32×150×6000 | 0,0288 м³ | 34 шт. | 31 м² |
| Доска обрезная | 32×180×6000 | 0,0346 м³ | 28 шт. | 31 м² |
| Доска обрезная | 32×200×6000 | 0,0384 м³ | 26 шт. | 31 м² |
| Доска обрезная | 32×250×6000 | 0,048 м³ | 20 шт. | 31 м² |
| Доска обрезная | 40×100×6000 | 0,024 м³ | 41 шт. | 25 м² |
| Доска обрезная | 40×120×6000 | 0,0288 м³ | 34 шт. | 25 м² |
| Доска обрезная | 40×150×6000 | 0,036 м³ | 27 шт. | 25 м² |
| Доска обрезная | 40×180×6000 | 0,0432 м³ | 23 шт. | 25 м² |
| Доска обрезная | 40×200×6000 | 0,048 м³ | 20 шт. | 25 м² |
| Доска обрезная | 40×250×6000 | 0,06 м³ | 16 шт. | 25 м² |
| Доска обрезная | 50×100×6000 | 0,03 м³ | 33 шт. | 20 м² |
| Доска обрезная | 50×120×6000 | 0,036 м³ | 27 шт. | 20 м² |
| Доска обрезная | 50×150×6000 | 0,045 м³ | 22 шт. | 20 м² |
| Доска обрезная | 50×180×6000 | 0,054 м³ | 18 шт. | 20 м² |
| Доска обрезная | 50×200×6000 | 0,06 м³ | 16 шт. | 20 м² |
| Доска обрезная | 50×250×6000 | 0,075 м³ | 13 шт. | 20 м² |
Сколько Досок 50х150х6000 в 1 кубе
📝 Брус и доска – один из древнейших строительных материалов, но он не теряет свою актуальность и сегодня. При этом стоимость этих пиломатериалов заставляет покупателей внимательно подходить к точности подсчета их необходимого количества.
При этом стоимость этих пиломатериалов заставляет покупателей внимательно подходить к точности подсчета их необходимого количества.
сколько обрезной доски в кубе
Сейчас можно найти во всемирной сети необходимые таблицы расчета нужного числа кубометров стройматериалов, но умелый хозяин должен уметь провести расчет самостоятельно.
Сколько в Кубе Досок 50 на 150 на 6000?
Как вы уже, наверное, поняли, расчет пиломатериалов проводится в кубических метрах. В то же время куб доски и бруса может иметь разные габаритные показатели. Поэтому для точной покупки нужно понимать размер этого куба для более точного расчета. Самый распространенный куб пиломатериалов имеет размеры 50х150х6000 мм.
Считаем нужный объем легко и просто
Проводить расчет кубометров доски или бруса очень легко. Для этого нужно иметь элементарные познания с геометрии, которые нам рассказывали еще в школе. Таким образом, для определения нужной кубатуры вам необходимо изначально умножить показатели ширины (l), толщины (s) и длины (b).
К примеру: s доски × l доски х b доски = 50 мм × 150 мм х 6000 мм = 45000 см/куб.
Мы помним, что кубометр равен 1000000 куб/см, то есть – 100 см х 100 см х 100 см.
Поэтому далее мы берем числовой показатель 1000000 и просто делим на кубатуру доски (бруса):
1000000 куб/см : 45000 куб/см = 22,22 штуки доски в одном кубе.
Сколько досок в 1 кубе таблица 6м:
| Размер доски | Объем 1-й доски | Досок в 1-ом кубе в штуках | Метров квадратных доски в 1 кубе |
|---|---|---|---|
| Пятидесятка | |||
| Доска 50х100х6000 | 0,03 м³ | 33 шт. | 20 м² |
| Доска 50х120х6000 | 0,036 м³ | 27 шт. | 20 м² |
| Доска 50х150х6000 | 0,045 м³ | 22 шт. | 20 м² |
| Доска 50х180х6000 | 0,054 м³ | 18 шт. | 20 м² |
| Доска 50х200х6000 | 0,06 м³ | 16 шт. | 20 м² |
| Доска 50х250х6000 | 0,075 м³ | 13 шт. | 20 м² |
Как вы видите, рассчитать необходимое количество 6-ты метровой доски очень легко. Теперь вы знаете, как определить сколько метровых досок в кубе. В зависимости от размера, вы просто подставляете нужные размеры в простую формулу и получаете готовый результат.
Сколько досок в 1 кубе пиломатериала, сколько штук в кубе — таблица и пример расчета
Для того чтобы посчитать, какое количество досок той или иной конфигурации содержится в одном кубическом метре, на нашем сайте доступна простая таблица расчетов. Воспользовавшись ею, вы сможете узнать, какое количество пиломатериалов понадобится вам для тех или иных нужд.
Воспользовавшись ею, вы сможете узнать, какое количество пиломатериалов понадобится вам для тех или иных нужд.
Итак, рассмотрим на примере обрезной доски размером 30х150х4000 мм:
1. Рассчитываем объем одной доски в м3
0,03 м · 0,15 м · 4 м = 0,018 м3
2. Рассчитываем количество досок в штуках на каждый кубический метр
1 м3 / 0,018 м3 = 55 шт./м3
3. Расчет метров квадратных в кубометре пиломатериала
1 м3 / 0,03 м = 33 м2/м3
Аналогичным образом можно производить расчет досок любой конфигурации, просто подставляя в формулу определенные значения. Эта формула будет полезна в случае, если вы желаете посчитать необходимое количество досок, нужное для вашего проекта.
Хотите перекрыть пол или определяетесь с количеством досок для перекрытия крыши? Мы поможем вам рассчитать нужный объем, руководствуясь простыми расчетами, представленными на этой странице.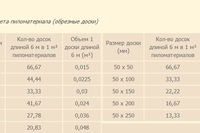
Таблица расчета шт. досок в кубе
| № | Размер | Объём доски (м3) | Штук в 1 м3 | Штук в 1 м2 |
| 1 | Доска 20х100х6000 мм | 0,012 м3 | 83 шт. | 50 м2 |
| 2 | Доска 20х120х6000 мм | 0,0144 м3 | 69 шт. | 50 м2 |
| 3 | Доска 20х150х6000 мм | 0,018 м3 | 55 шт. | 50 м2 |
| 4 | Доска 20х180х6000 мм | 0,0216 м3 | 46 шт. | 50 м2 |
| 5 | Доска 20х200х6000 мм | 0,024 м3 | 41 шт. | 50 м2 |
| 6 | Доска 20х250х6000 мм | 0,03 м3 | 33 шт. | 50 м2 |
| 7 | Доска 25х100х6000 мм | 0,015 м3 | 67 шт. | 40 м2 |
| 8 | Доска 25х120х6000 мм | 0,018 м3 | 55 шт. | 40 м2 |
| 9 | Доска 25х150х6000 мм | 0,0225 м3 | 44 шт. | 40 м2 |
| 10 | Доска 25х180х6000 мм | 0,027 м3 | 37 шт. | 40 м2 |
| 11 | Доска 25х200х6000 мм | 0,03 м3 | 33 шт. | 40 м2 |
| 12 | Доска 25х250х6000 мм | 0,0375 м3 | 26 шт. | 40 м2 |
| 13 | Доска 30х100х6000 мм | 0,018 м3 | 55 шт. | 33 м2 |
| 14 | Доска 30х120х6000 мм | 0,0216 м3 | 46 шт. | 33 м2 |
| 15 | Доска 30х150х6000 мм | 0,027 м3 | 37 шт. | 33 м2 |
| 16 | Доска 30х180х6000 мм | 0,0324 м3 | 30 шт. | 33 м2 |
| 17 | Доска 30х200х6000 мм | 0,036 м3 | 27 шт. | 33 м2 |
| 18 | Доска 30х250х6000 мм | 0,045 м3 | 22 шт. | 33 м2 |
| 19 | Доска 32х100х6000 мм | 0,0192 м3 | 52 шт. | 31 м2 |
| 20 | Доска 32х120х6000 мм | 0,023 м3 | 43 шт. | 31 м2 |
| 21 | Доска 32х150х6000 мм | 0,0288 м3 | 34 шт. | 31 м2 |
| 22 | Доска 32х180х6000 мм | 0,0346 м3 | 28 шт. | 31 м2 |
| 23 | Доска 32х200х6000 мм | 0,0384 м3 | 26 шт. | 31 м2 |
| 24 | Доска 32х250х6000 мм | 0,048 м3 | 20 шт. | 31 м2 |
| 25 | Доска 40х100х6000 мм | 0,024 м3 | 41 шт. | 25 м2 |
| 26 | Доска 40х120х6000 мм | 0,0288 м3 | 34 шт. | 25 м2 |
| 27 | Доска 40х150х6000 мм | 0,036 м3 | 27 шт. | 25 м2 |
| 28 | Доска 40х180х6000 мм | 0,0432 м3 | 23 шт. | 25 м2 |
| 29 | Доска 40х200х6000 мм | 0,048 м3 | 20 шт. | 25 м2 |
| 30 | Доска 40х250х6000 мм | 0,06 м3 | 16 шт. | 25 м2 |
| 31 | Доска 50х100х6000 мм | 0,03 м3 | 33 шт. | 20 м2 |
| 32 | Доска 50х120х6000 мм | 0,036 м3 | 27 шт. | 20 м2 |
| 33 | Доска 50х150х6000 мм | 0,045 м3 | 22 шт. | 20 м2 |
| 34 | Доска 50х180х6000 мм | 0,054 м3 | 18 шт. | 20 м2 |
| 35 | Доска 50х200х6000 мм | 0,06 м3 | 16 шт. | 20 м2 |
| 36 | Доска 50х250х6000 мм | 0,075 м3 | 13 шт. | 20 м2 |
Брус 50х150х6000 сколько штук в кубе
Пользовательские Оптическое Стекло 5 мм 50/50 Луч Splitter Cube Prism
Q1. Вы фабрика?
А1. Да, мы являемся профессиональным производителем оптических компонентов, у нас более 20 лет опыта работы в области оптической холодной обработки.
Q2. Что такое MOQ вашей продукции?
А2. Нет MOQ для клиента, если наш продукт есть в наличии,
Q3: Могу ли я изготовить продукцию на заказ в соответствии с моими требованиями?
А3.Да, мы можем изготовить на заказ материал, технические характеристики и оптическое покрытие для ваших оптических компонентов.
Q4. Как я могу получить образец от вас?
А4. Просто отправьте нам свои требования, и мы отправим образцы соответственно.
Q5. Сколько дней образцы будут закончены? Как насчет массовых продуктов?
А5. Как правило, нам нужно 1 ~ 2 дня, чтобы закончить производство образца. Что касается массовых продуктов, это зависит от вашего заказа.
Q6.Какое время доставки?
А6. (1) Для инвентаря: срок поставки 1-3 рабочих дня.
(2) Для изделий по индивидуальному заказу: срок поставки от 7 до 25 рабочих дней. По количеству
Q7. Как вы контролируете качество?
A7. Более чем в четыре раза проверять качество в процессе производства, мы можем предоставить отчет о проверке качества.
Q8. Как насчет вашего производства оптических линз в месяц?
A8. Около 20000 шт. / Месяц.Согласно требованию детали
Как разгадать кубик Рубика с завязанными глазами
Решение кубика Рубика — главное достижение. То, что на самом деле не так много людей делают. Как только вы научитесь решать куб, вы поймете, насколько это просто. Будучи спидбакером, мне иногда трудно понять, что многие считают его почти невозможным.
Однако, как только вы овладеете кубом, вы захотите большего. Конечно, вы можете подняться на большие кубы, такие как 4×4, 5×5 или дальше. Вы можете перейти к более простым головоломкам, таким как 2×2 или Pyraminx.Но для тех из вас, кто хочет дополнительного испытания, чего-то, что действительно проверяет вашу память и способности, вы можете попытаться решить куб с завязанными глазами.
Решения с завязанными глазами популярны среди спидкуберов, но есть много людей, которым просто нравится делать это для развлечения. Большинство людей считают, что для решения проблемы со зрительным кубом требуется поразительный объем памяти, не говоря уже о том, чтобы решать его с завязанными глазами. Но на самом деле это так же просто, если не проще.
Нет ничего более ценного, чем снять повязку и увидеть решенный кубик Рубика перед собой.В этой статье я собираюсь научить вас, как это сделать.
Old Pochmann
Old Pochmann (или OP), является одним из старейших методов с завязанными глазами на сегодняшний день. Он был разработан Штефаном Почманном, который в 2004 году установил Немецкий национальный рекорд 3×3 с завязанными глазами. Ему удалось побить свой собственный рекорд 4 раза за 23 месяца, прежде чем он проиграл Томасу Кону. Он сократил NR с 35 минут до 7.
Он был разработан Штефаном Почманном, который в 2004 году установил Немецкий национальный рекорд 3×3 с завязанными глазами. Ему удалось побить свой собственный рекорд 4 раза за 23 месяца, прежде чем он проиграл Томасу Кону. Он сократил NR с 35 минут до 7.
В наши дни Old Pochmann по-прежнему используется многими. Тем не менее, ускорители, которые соревнуются в разгадывании куба с завязанными глазами как можно быстрее, переключились на новые и более быстрые методы.Но Old Pochmann по-прежнему способен достигать времени менее 2 минут, если вы заинтересованы в быстром разрешении с ним.
Алгоритмы
Решение куба с завязанными глазами требует значительно меньше алгоритмов, чем зрячее. Используя метод Old Pochmann, вы можете решить куб всего за пять алгоритмов. Если вы знаете, как решить обнаруженный куб, вы, возможно, уже знаете некоторые из них из продвинутого учебника Рубика по кубу:
— Все изображения показывают верхнюю грань куба, так как это алгоритмы PLL — Пожалуйста, прочитайте расширенную нотацию Кубика Рубика, если вы не знаете, что означают буквы.
T Перестановка
R U R ’U’ R ’F R2 U’ R ’U’ R U R ’F’
Этот алгоритм переключает два крайних правых угла и ребро между ними с ребром напротив него.
Ja Перестановка
R U R ’F’ R U R ’U’ R ’F R2 U’ R ’U’
Этот алгоритм переключает два крайних правых угла и ребро между ними, причем ребро примыкает к передней грани.
Jb Перестановка
y2 L ’U2 L U L’ U2 R U ’L U R’ y2
Этот алгоритм переключает два крайних правых угла и ребро между ними, причем ребро примыкает к задней поверхности (важно отметить, что для выполнения этого алгоритма вам необходимо повернуть куб, чтобы вы удерживали куб в показанной ориентации вправо, прежде чем делать алгоритм.Затем вам нужно повернуть назад, чтобы продолжить.
Y Перестановка
F R U ’R’ U ’R U R’ F ’R U R’ U ’R’ F R F ’
Этот алгоритм заменяет нижний правый угол на верхний левый угол и два верхних левых края. Важно отметить, что этот алгоритм работает не совсем так, но позже вы поймете, почему.
Ra Перестановка (алгоритм четности)
лет L U2 L U U L L F L L U U L L L U U
Этот алгоритм меняет местами два задних угла и два соседних ребра спереди и справа.Этот алгоритм требует ротации до и после, потому что части, которые вам нужно поменять местами, находятся не прямо перед вами. Кроме того, движение U в конце не должно быть пропущено, иначе верхний слой будет смещен по U, что разрушит все, что вы запомнили.
Обозначение
Нотация очень важна для решения с завязанными глазами, так как вам нужно знать, куда вы собираетесь отправлять свои произведения. Сначала вам нужно выбрать свою ориентацию. Я рекомендую иметь желтый сверху и оранжевый спереди, так как это самая популярная ориентация.
С завязанными глазами кубиками мы работаем с наклейками вместо кусочков. Решая часть, это должно быть в правильной ориентации. Недостаточно просто помнить само произведение, так как есть вероятность, что оно будет перевернуто на свое место. Поэтому на каждой наклейке на каждом лице есть буква (кроме наклейки в центре).
Вам нужно назначить букву каждой наклейке на вашем кубе. Я показал мою схему надписи ниже. Вы должны помнить, что большинство ориентаций, которые вы видите, не будут одинаковыми, когда вы решаете, потому что, если красное лицо сзади, нужно поменять схему букв.Поскольку буквы и углы решаются отдельно, вы можете иметь одну и ту же букву для двух наклеек.
Эта диаграмма может показаться запутанной. Если хотите, посмотрите на каждое лицо так, как будто вы идете по часовой стрелке вокруг него с двумя написанными буквами.
Например —
Угол YBO имеет буквы C, I и F соответственно.
Край OW имеет буквы G и U соответственно.
Буфер
Старый Pochmann сильно зависит от части буфера, которая используется в качестве отправной точки.Для решения края буфер является краем UR. Таким образом, используя ориентацию, рекомендованную выше (желтый сверху, оранжевый сверху), край буфера будет краем YB, а угол буфера будет углом YRG.
Old Pochmann работает так, как будто вы используете буферный элемент, чтобы «выстрелить» в правильное положение в правильном положении.
Края
Итак, теперь мы знаем основы ОП, давайте начнем!
Сначала сделайте эту схватку на своем кубе —
R2 B2 D R2 D ‘U’ R2 F2 L2 B2 D2 F U2 R ‘F U’ L2 B L F2 U
Не забудьте карабкаться с белым сверху и зеленым спереди.
Ваш куб должен выглядеть так:
Когда вы впервые смотрите на куб, первое, что вам нужно сделать, это повернуть его так, чтобы он был в вашей предпочтительной ориентации (для этой схватки, пожалуйста, используйте ориентацию желтый сверху, оранжевый спереди). Далее нужно взглянуть на край буфера. Какой край находится в буферной позиции: оранжевый-зеленый. Что еще более важно, оранжевая наклейка сверху.
Ваша следующая задача — найти оранжево-зеленую позицию (куда пойдет оранжево-зеленый край, когда куб будет решен).Вы можете видеть, что это пошло бы в переднем левом положении.
Но поскольку это наклейка ORANGE сверху, вам нужно стрелять в положение ORANGE. Край в настоящее время в оранжево-зеленой позиции является бело-синим краем.
Используя приведенную выше схему букв, мы можем видеть, что это будет буква H. Итак, мы запомним эту букву и продолжим.
Представь, что ты поменял эти два края. Теперь бело-синий край будет в вашем буфере с белым сверху. Вы должны видеть это, потому что, надев повязку, вы не можете полагаться на зрение, чтобы сказать вам, где находится наклейка.Так, где должен идти бело-синий край? Бело-голубая позиция, конечно. Это позиция DR. Но помните — мы стреляем в белую сторону позиции, а не в синюю сторону. Поэтому, используя буквенную схему, мы можем видеть, что наше следующее письмо — V.
Теперь у вас есть две буквы. H и V. Если вы продолжите так, вы, скорее всего, забудете буквы. Таким образом, мы связываем буквы с людьми, объектами, местами, чем угодно. Вам просто нужно что-то придумать, чтобы, когда вы вспомните это позже, вы сразу вспомнили буквы H и V.Лучший способ убедиться, что ваши письма запоминаются эффективно, — запоминать их по две за раз.
Если вы планируете сделать это быстро, вы не сможете потратить 30 секунд на размышления о великолепном, ярком изображении. Вам нужно придумать прилично запоминающийся образ и двигаться дальше. Первое, что придет в голову, это HooVer. Так что я думаю о пылесосе. Оставшаяся часть запоминания будет определять, нужно ли вам думать о том, что пылесос делает что-либо, или просто о простом пылесосе.
Теперь ты притворяешься, что только что выстрелил в бело-синий край.Какая фигура сейчас в этой позиции? Красно синий. Но, опять же, вы стреляли в БЕЛЫЙ, что означает, что наклейка, которая находится сверху в вашем буфере, теперь будет красной. Итак, вы ищите красно-синюю позицию, в данном случае это BR. Используя буквенную схему, вы можете видеть, что красная наклейка в этой позиции имеет букву P. Итак, вы помните P.
Что сейчас в вашем буфере? Бело-оранжевый. Ищите бело-оранжевую позицию. Это ст. Теперь найдите букву, связанную с белой наклейкой (потому что белая сверху).Письмо U.
Это действительно для краев. Все, что вы делаете, это прыгаете от края до края, решая их по ходу, один за другим, запоминая буквы на своем пути.
Наши текущие письма — HVPU. У нас есть HooVer, но чем может быть PU? Вы можете подумать о другом объекте (наиболее очевидным из которых является poo) или о прилагательном для описания HooVer. Я бы наверное запомнил PU как PUshes. Следующие две буквы укажут, что именно пылесос толкает в моей голове.
Пока то, что вы запоминаете, имеет смысл, на самом деле не имеет значения, какие у вас буквы. Вы свободны исследовать свое собственное воображение, чтобы найти вещи, которые напоминают вам о двух письмах, которые вы пытаетесь запомнить.
Хорошо, давай пропустим. Если вы выполните описанные выше шаги, вы запомните буквы — HVPUEFTXDW (мое запоминание
. Как решить 3x3x3 кубик Рубика — Стандартный куб — 3×3 Кубик Рубика
Продолжая эту серию уроков, мы увидим теперь Как решить 3x3x3 кубик Рубика .
Чтобы научиться решать кубик Рубикса 3×3, не сложнее, чем научиться решать кубик Рубикса 2×2.
В этом руководстве вы найдете всю необходимую информацию для решения стандартного куба.
Однако желательно сначала прочитать, как решить младший куб, поскольку методы, применяемые для разрешения младшего куба, будут очень полезны для решения стандартного куба.
Все выученные движения для разрешения младшего куба будут использоваться в разрешении стандартного куба, и будет добавлено еще несколько, достигая таким образом постепенную кривую обучения.
Оглавление
• Как решить кубик Рубикса 3x3x3
• Кусочки и слои
• Описание алгоритма
• Шаг 1, края нижнего слоя
• Шаг 2, Углы нижнего слоя
• Шаг 3, края среднего слоя
• Шаг 4, последний слой края
• Шаг 5, Переставьте края верхнего слоя
• Шаг 6, Ориентируйте углы верхнего слоя
• Шаг 7, Перестановка углов верхнего слоя
• Решить кубик Рубикса 3x3x3
• Шаг 1, края нижнего слоя
• Цвет лицевой стороны на верхней стороне лица
• Пухлый цвет лица по краям
• Край в среднем слое
• Край в нижнем слое
• Шаг 2, Углы нижнего слоя
• Цвет пуха на лицевой стороне
• Цвет пуха внизу на правой стороне
• Цвет пухлого лица на верхней части лица
• Угловой элемент в нижнем слое
• Шаг 3, края среднего слоя
• Кромка вправо
• Кусок кромки слева
• Шаг 4, последний слой края
• Линия
• L
• Точка
• Шаг 5, Переставьте края верхнего слоя
• Перестановка трех граней против часовой стрелки
• Перестановка трех граней по часовой стрелке
• Шаг 6, Ориентируйте углы верхнего слоя
• Цвет верхней грани на правой стороне
• Цвет верхней поверхности спины
• Шаг 7, Перестановка углов верхнего слоя
• Перестановка трех углов против часовой стрелки
• Перестановка трех углов по часовой стрелке
Как решить кубик Рубика 3x3x3
Чтобы понять, как решить 9503 кубика Рубика 3x3x3 , необходимо ознакомиться с обозначениями.Если вы этого не знаете, пожалуйста, прочитайте «Как решить кубик Рубика», прежде чем продолжить.
Сначала будет показано описание алгоритма, а затем движения.
Для целей следующего урока будет выбран ряд цветов для граней, вы можете выбрать другие.
Имейте в виду, что цвет центральной части определяет цвет лица.
Как решить кубик Рубикса 3x3x3 — описание алгоритма
Алгоритм разделен на семь этапов.На каждом шаге выполняется серия ходов, чтобы решить куб. Серия повторяется (неразрешенные кубы) до завершения шага.
(Для лучшего понимания описания черные наклейки представляют не относящийся к этому цвету цвет.)
Шаг 1, края нижнего слоя
Первый шаг — сделать крест на нижнем слое.
Убедитесь, что второй цвет на каждом краю соответствует цвету центрального кубика на каждой боковой грани.
Шаг 2, Углы нижнего слоя
Поместите угловые элементы в нужное положение на нижнем слое.
Когда все углы на месте, нижний слой решен.
Шаг 3, Кромки среднего слоя
Поместите кромки в средний слой.
Когда все ребра на месте, средний слой решен.
На этом этапе нижний слой и средний слой завершены, это называется F2L ( первые 2 слоя )
Шаг 4, края последнего слоя
Первый шаг к решению последнего слоя — сделать крест на верхней грани, не заботясь о других цветах по бокам.
Шаг 5, Перестановка кромок верхнего слоя
Если ребра не находятся в своих решенных положениях, следующим шагом будет правильное расположение ребер.
Шаг 6, Ориентация углов верхнего слоя
Поместите угловые части на верхнем слое, не заботясь о других цветах по бокам.
Шаг 7, Перестановка углов верхнего слоя
Если углы не находятся в своих решенных положениях, следующим шагом будет правильное расположение углов.
Поздравляем! Вы решили куб.
Как решить кубик Рубикса 3x3x3 — алгоритм
Теперь, когда вы поняли метод, пришло время применить его на практике.
Шаг 1, края нижнего слоя
Выберите цвет для нижней грани и цвет для лицевой стороны: (давайте возьмем желтый и красный)
Найдите в верхнем слое кусок края обоих цветов.
Возможны два состояния: цвет «Вниз» (желтый) находится на верхней грани, цвет «Вниз» (желтый) — по краям (при необходимости поверните верхний слой).
Используйте одну из следующих процедур для решения куба:
Ход [R] восстанавливает Крайнюю Часть, которая, возможно, была удалена с ее места.
Если кусок края находится в среднем слое или в нижнем слое, но не решен, переместите его на верхний слой.
Ход [R ‘] восстанавливает Крайнюю Часть, которая, возможно, была удалена с ее места.
Выберите другой цвет для передней грани и повторяйте процедуру до завершения креста на нижней грани.
Шаг 2, Углы нижнего слоя
Найдите в верхнем слое угловую фигуру цвета нижней грани (желтая).
Посмотрите на два других цвета фигуры (например, на красный и синий), поместите угловую фигуру (поверните верхний слой) между двумя центральными фигурами одинаковых цветов.
Есть три возможных состояния:
Если угловой элемент находится в нижнем слое, переместите его в верхний слой и используйте описанную выше процедуру.
Шаг 3, Кромки среднего слоя
Найдите в верхнем слое кусок кромки, который не имеет цвета верхней грани (белого), если не видите захваченные нижние края.
Выберите цвет для передней грани (красный), поверните верхний слой, чтобы он соответствовал цвету краевой части с тем же цветом центральной части.
Есть два возможных состояния:
В случае захвата краев выполните одну из описанных выше процедур, чтобы заменить захваченный край краем из верхнего слоя.
Если, например, зелено-красная кромочная часть захвачена в среднем слое, как показано, выполните первую процедуру, чтобы заменить ее серой кромочной частью.Как только зелено-красная кромка окажется на верхнем слое, продолжайте как обычно.
(серая фигура представляет любые двухцветные кромки)
Шаг 4, края последнего слоя
Существует три возможных состояния: точка, линия, L.
Определите состояние и применяйте некоторые из вышеуказанных процедур, пока не будет сформирован крест.
Шаг 5, Перестановка краев верхнего слоя
Если при повороте верхнего слоя цвет краевых частей совпадает с цветом центральных частей, перейдите к следующему шагу, если это не так, попробуйте выровнять верхний слой так, чтобы что решена только одна Edge Piece (если нет, см. ниже).
Есть два возможных состояния:
Если невозможно расположить верхний слой так, чтобы был решен только один край, выполните одну из описанных выше процедур, чтобы получить один крайний слой сверху, а затем выполните то же, что и раньше.
Шаг 6, Ориентация углов верхнего слоя
Угловой элемент, который должен быть ориентирован, не имеет цвет верхней грани (белый).
Определите углы, которые должны быть ориентированы, возможно, придется крутить 2, 3 или 4 угловых элемента.
Поверните верхний слой так, чтобы угловой элемент, который должен быть ориентирован, находился сзади справа.
Возможны два состояния: цвет верхней грани (белый) на правой стороне или цвет верхней грани (белый) на задней стороне.
После ориентации первой угловой детали первые два слоя скремблируются.
НЕ ВРАЩАЙТЕ КУБ, ОБЕСПЕЧИВАЙТЕ ПЕРЕДНУЮ ЛИЦУ .
Поверните верхний слой так, чтобы следующая угловая фигура, которая должна быть ориентирована, находилась сзади и справа, а затем продолжила то же, что и раньше.
Как только вы скрутите все углы, первые два слоя восстановятся.
ПРИМЕЧАНИЕ: Чтобы эта процедура работала правильно, вам нужно два, три или четыре угла, которые должны быть ориентированы.
Если у вас есть только один угол, плохо ориентированный, выполняя следующее движениями четыре угловые части должны быть ориентированы.
(Поместите неправильную угловую часть в передний правый)
Теперь перейдите к шагу 6 в обычном режиме.
Шаг 7, Перестановка углов верхнего слоя
Поверните верхний слой так, чтобы угловой элемент находился в своем решенном положении (если нет, см. Ниже).
Поверните куб в своих руках, чтобы удерживать его с разрешенным углом в переднем левом положении.
Есть два возможных состояния:
Если невозможно найти угловой элемент в его решенном положении, выполните одну из приведенных выше процедур, чтобы получить его.
Теперь вы знаете Как решить кубик Рубикса 3x3x3 .
Как приготовить кубик Рубика
Хороший друг из Финляндии, Аксели Пален, привел интересную тему: Как приготовить куб?
Конечно, можно использовать такие методы, как вращение граней куба в любом направлении в течение некоторого времени, или дать кому-то еще, чтобы он вращался для нас.
Хотя нам может показаться, что куб скремблирован, в большинстве случаев, когда мы скремблируем решенный куб, он остается «частично собранным», потому что мы всегда выполняем избыточные последовательности.
Есть ли правильный способ шифрования куба?
Да. В соревнованиях используются алгоритмы (схватки) для обеспечения справедливости между конкурентами.
Процедура выглядит следующим образом:
- Произведено случайное количество движений (от 25 до 30)
- Для каждого движения выбирается случайная грань (U, D, L, R, F, B) и ход (X, X ‘X2)
- Исключения:
- а) Следующее движение не должно быть того же лица, что и предыдущий
- b) Если две грани перемещаются в одной плоскости последовательно, эти грани отбрасываются для следующего хода (то есть: перемещение n -> U; перемещение n + 1 -> D; перемещение n + 2 -> выбор между: L, R, F, B)
Алгоритм
Компания Akseli разработала веб-приложение для правильного шифрования кубика Рубика, которое я рекомендую вам посетить, добавить в закладки и рассказать друзьям-фанатам кубика Рубика.
________________________________________________________________
Подтверждение: Содержание от Darkside
________________________________________________________________
,
Доска 40 150 сколько штук в кубе. Доска обрезная. Сколько метров в кубе
домой → Советы → Доска 40 150 сколько штук в кубе. Доска обрезная. Сколько метров в кубе
Покупать материалы на глазок — ерунда, и ни один уважающий себя хозяин этим не пойдет. Чтобы правильно сделать смету и оценить, сколько обернется строительство или капитальный ремонт, нужно определить, сколько потребуется того или иного продукта. С плитами сложнее — они не продаются по отдельности, а продаются (по мере хранения) партиями, объем которых выражается в м³.Но количество штук, как правило, «привязано» к покрытой площади, то есть к м². Разберемся, как определить, сколько досок будет в одном кубе.
Почему доски ровно 4 и 6 метров? Приведенная ниже процедура расчета не изменяется для любой длины. Дело в том, что указанные параметры являются наиболее «ходовыми». Производители ориентируются на габариты платформ и грузовых вагонов, поэтому им выгоднее поставлять доски длиной 6 метров. Но покупателя больше интересуют четырехметровые доски, так как для их перевозки достаточно грузовика с удлиненным кузовом.
Для перевозки 6-ти метровых досок необходим автопоезд; Следовательно, стоимость доставки пиломатериалов на участок увеличится. Да и маневренность таких машин существенно ограничена. Например, доставлять доски на нем на дачу бессмысленно, учитывая узость аллей.
Порядок расчета количества досок в кубе
Вам просто нужно вспомнить среднюю школу. Так называемый «куб» (обычное название меры объема) — это произведение линейных параметров любого объемного объекта.То есть его длина, ширина и высота (в данном случае толщина).
- Произведен замер граней одной из досок в стопке. Получается ширина и толщина. Длина известна — 4 или 6 м.
- Все измеренные параметры переведены в одно измерение. Поскольку речь идет о кубе, то есть м3, все они (включая ширину и толщину) указаны в метрах.
- Определена «кубатура» заготовки.
- 1 м³ делим на полученное значение.Результат — количество досок в кубе.
В числителе дроби ставить ровно 1. Хранение досок осуществляется разными способами, и пиломатериалы в таком количестве не всегда требуются. Если штабель 0,8 кубометра, то это его объем.
Пример. Покупается доска 6 м, шириной 25 мм, шириной 20 см, в количестве одного куба.
- Переводим значения в метры: толщина — 0,025, ширина — 0.2.
- Определяем кубатуру доски: 6 х 0,2 х 0,025 = 0,03 м³.
- Рассчитываем количество образцов — 1: 0,03 = 33, (3).
Калькулятор количества и объема пиломатериалов
Если полученное значение является дробным, результат всегда округляется до целого числа. То есть во внимание принимаются только числа до запятой. Это общепринятая норма!
Эти таблицы помогут определить примерное количество досок в кубе, не прибегая к расчетам.
- Алгоритм расчета одинаковый для всех пиломатериалов данной группы вне зависимости от их характеристик — породы древесины, степени сушки.
- Табличные значения являются чисто ориентировочными, так как они не совсем корректно отражают реальное количество досок в кубе. Во-первых, многое зависит от укладки стопок, то есть от того, насколько плотно будут доски. Во-вторых, ничего не говорится о качестве обработки заготовок (обрезаны они или нет).В-третьих, не факт, что при внимательном осмотре определенное количество плат не будет забраковано из-за обнаруженных дефектов. Поэтому всегда необходимо уменьшать их количество, полученное расчетным путем. Если доска обрезная — примерно на 10%, в случае необрезная — на 15-20%.
Для изготовления пиломатериалов используются разные виды деревьев, например, обрезные доски. На такой доске нет коры, что делает ее пригодной для строительства и изготовления мебели.
Основное отличие доски обрезной от других видов — полное отсутствие подборщика, коры, это отличает ее от необрезной с подборщиком
Самыми популярными деревьями, из которых делают обрезную доску, обычно являются хвойные породы
Тип плиты по виду материала (сырья)
В зависимости от содержания влаги в ней плита может быть влажной или сухой.На качество готовой доски большое влияние оказывает порода древесины. Каждое дерево имеет свои уникальные характеристики, но всех их объединяет природное происхождение и экологическая чистота.
Основные размеры обрезного пиломатериала:
Стандартная длина 6,0 метра (может быть 4,0 и 3,0 м.)
Что касается строительства, то здесь чаще всего используют доску из хвойных пород дерева. Эти материалы имеют более плотную структуру и обладают отличной теплопроводностью.
Сортировать обрезную доску:
Кроме того, сосновая доска обладает антисептическими свойствами, что делает ее идеальным материалом для внутренней отделки.К тому же такая доска стоит недорого, что также привлекает разработчиков использовать ее при строительстве дома.
Доска обрезная при строительстве домов из бруса
При монтаже используется доска обрезная для:
черновая отделка (под сайдинг, гипсокартон и др.)
стропила
Черновой пол (на него укладывается шпунт)
При изготовлении обрезной доски используются разные варианты ее распила. Наивысшее качество — это радиальный распил, в котором используется пропитанный смолой прочный бревенчатый стержень.В результате такая доска не подвергается деформации при сушке. Цена на такую доску будет выше, так как для ее изготовления уходит лучшая часть бревна.
При полурадиальном распиле значительно сокращаются отходы материала, что снижает стоимость готовой обрезной доски. Толщина доски при растворении тоже разная. Доска обрезная может производиться 25, 30, 40 мм. Самая качественная и дешевая доска получается при тангенциальном распиле. Такой материал склонен к набуханию и усадке, но такой способ резки дает наибольший выход материала, что значительно снижает его цену.
Цена обрезной доски принимается за куб или 1 метр квадрат
| Имя | Размеры, мм | Цена, руб / м3 * |
| Доска обрезная | 25-200 x 6000 | 5700 |
| Доска обрезная | 25- 200 x 4000 | 5600 |
| Доска обрезная | 25-70 x 2000,3000 | 5200 |
Разница в стоимости между обрезным или необрезным участком составляет 1500 рублей за кубометр, подумайте, стоит ли экономить
Доска обрезная чаще всего находит применение при производстве строительных работ и при изготовлении мебельных изделий.При покупке такого материала необходимо выбирать только сухую доску, иначе в будущем она может подвергнуться деформации.
Сколько кубиков в разделочной доске
25x150x6000 (длина — 6000, высота — 25, ширина — 150)
объем одной доски 1шт = 0,0225 куб. метров.
в 1 куб = 44,4 шт. по факту — 44 шт. доски .
50x150x6000 (длина — 6000, высота — 50, ширина — 150)
объем одной платы 1шт = 0.045 куб. метр
в 1куб = Доска 22,2 шт
Размер доски, мм
Количество досок в 1 кубометре, шт
- 25x150x4000 66,7 шт.
- 40x150x4000 41,6 шт.
- 20x100x6000 83,3 шт.
- 25x100x6000 66,7 шт.
- 40x100x6000 41,6 шт.
- 50x100x6000 33,3 шт.
- 25x150x6000 44,4 шт.
- 30x150x6000 37,04 шт.
- 40x150x6000 27,8 шт.
- 50х150х6000 22.2 шт.
- 25x200x6000 33,3 шт.
- 40x200x6000 20,8 шт.
- 50x200x6000 16,7 шт.
Подробнее и для всех размеров в таблице
Кстати, таким образом, зная количество штук в кубе обрезной доски, можно рассчитать стоимость и доски за одну штуку, это необходимо, если вы покупаете поштучно или покупаете, если вам не хватило количество.
Общепринятой мерой измерения древесных материалов является кубический метр.Чаще всего в кубометрах измеряются пиломатериалы — обрезные, необрезные, строганные и другие древесные материалы. Другими словами, 1 м 3 — это объем, равный 1 м по длине, ширине и толщине.
Сколько кубиков в одной доске 40x150x6000
Расчет кубатуры древесины зависит от ее 2 характеристик, в частности от того, обрабатывается она или нет.
Чтобы узнать, сколько кубиков в одной доске 40x150x6000 (обрезной), воспользуйтесь таблицей расчета или следующей формулой:
В = a × b × l, где
- a — высота;
- b — ширина;
- л — это длина.
Объем исчисляется в кубических метрах, поэтому все значения следует предварительно перевести в миллиметры в метры. Соответственно, толщина этого материала — 0,04 м, ширина 0,15 м, длина 0,6 м. Следующим шагом будет прямой расчет кубатуры:
- В = 0,04 × 0,15 × 6 = 0,036
Соответственно, в одну кромочную 6-метровую «сорок» — 0,036 м 3.
Для необрезанных точных табличных данных нет. Средняя кубатура деревянного элемента сечением 40 х 6000 — 0.05 м 3.
Сколько досок в кубе
Пиломатериалы обрезные 40 × 150 × 6000 широко используются в строительстве и мебельном производстве, для изготовления тары, в интерьере и других целях. Чтобы узнать, сколько штук «сорок» в кубе, нужно знать кубатуру 1-й доски. Дальнейший расчет не представляет особой сложности, достаточно воспользоваться специальным калькулятором или следующей формулой:
К = 1 м 3 / Vd, где Vd — м 3 доски.
В нашем случае расчет будет выглядеть так:
К = 1/0.036 = 27,777 шт.
Соответственно в 1 кубометре пиломатериалов сечением 40 × 150 × 6000 будет примерно 28 шт. Лучше округлить.
Сколько метров в кубе
В 1 кубометре пиломатериалов может быть разное количество квадратных метров. Этот показатель зависит от толщины изделия. Поэтому, чтобы узнать, сколько метров в одном кубе дерева необходимо 1 м3 разделить на толщину.
Т = 1 / а, где:
В нашем примере толщина пиломатериала 40 мм, что равно 0.04 м соответственно. Подставляем в формулу и получаем:
Т = 1 / 0,04 = 25 м 2
В итоге в 1 кубометре доски толщиной 4 сантиметра будет 25 м 2.
Кубатура одной доски обрезной толщиной 40 мм
Кубический объем обрезного пиломатериала 40 х 150 х 6000, а также количество досок и квадратных метров в 1 кубометре можно увидеть в таблице. Поможет правильно определить необходимый объем стройматериалов, чтобы не нести лишних затрат при их покупке.
При проведении строительных работ по возведению жилого дома специалист должен выполнить большое количество различных задач, одна из которых: составление и расчет сметной стоимости перед окончательной отделкой жилого дома. В обязательном порядке рассчитать необходимое количество различных строительных материалов, что сделать довольно сложно. Поэтому такие знания — сколько досок в кубе, очень важно для специалиста, который занимается строительством жилого дома и хочет выполнить работу максимально качественно и быстро в срок.
Торговый клуб: существующие типы досок
Чтобы подсчитать, сколько досок находится в кубе, нужно знать не только, что именно означает куб, но и важно понимать, что существуют разные типы досок. досок и что можно приобрести на современном рынке для различных строительных работ. Следует отметить, что куб практически всех материалов, независимо от типа материала, рассчитывается одинаково, то есть по одной конкретной методике.Разновидности досок никак не влияют на расчет кубатуры этого строительного материала.
К необрезным видам пиломатериалов относятся: брус, различные обрезные доски, а также необрезные доски (они являются исключением при расчете кубатуры, потому что этот процесс происходит несколько иначе). К рифленым типам (имеющим специальные пазы для заделки швов) относятся: современная вагонка, сруб, напольный материал, а также имитация натурального дерева. Выбирая для покупки рифленый вид стройматериала, тогда нужно будет обратить внимание, что при расчете используется только рабочая ширина доски без шипа.Если говорить о срубе (имитация бревен), то при расчете кубатуры берется только толщина в ее наивысшей точке.
Сколько досок в 1 кубе: расчет
Любой еще со школьных времен понимает, как производится расчет кубатуры. Для этой процедуры необходимо рассчитать такие величины, как: длина, ширина и высота. По аналогичному принципу рассчитывается кубатура 1 доски. Рекомендуется при выполнении таких расчетов перевести все доступные значения в метры.Кубатура из 1 доски сечением 150х20 мм. и длиной 6 метров он рассчитывается следующим образом: 0,15 умножается на 0,02 и на 6, так что кубатура этой доски будет 0,018 кубометра.
Применяем формулу объема V = L * h * b (где L — длина, h — высота, b — ширина).
L = 6,0; h = 0,02; b = 0,15.
Таким образом, V = 6,0 * 0,02 * 0,15 = 0,018 м 3.
Для определения количества досок в одном кубе: 1 м 3 разделить на кубатуру (объем одной доски).
1 м 3 / В = N шт.
1 м 3 / 0,018 м 3 = 55,55 шт.
Таким образом, количество досок в одном кубе 55,5 штук.
Узнать стоимость того или иного вида плиты достаточно просто, зная ее объем: 0,018 умножаем на цену 1 кубометра. Если 1 кубик доски определенного типа стоит, например, 5500 рублей, то стоимость будет 99 рублей. На этом этапе расчетов есть некоторая уловка продавцов и менеджеров в строительных магазинах, потому что кубатура материала округляется до некоторых целых значений.
Такое округление может привести к тому, что цена 1 доски (при стоимости 1 куба 5500) будет совсем другими значениями. Помимо всего этого, следует отметить, что различные строительные плиты, которые составляют номинальную длину 6 метров, на самом деле имеют длину 6,1 — 6,2 м, что не учитывается при продаже этого стройматериала. Это касается и приобретения значительного количества досок. Это довольно хорошо видно, если, например, используется доска 150х20 мм.Количество досок в кубе — значение 55,5 шт. Но, в кубе считается 55 штук, что при подсчете будет значением 0,99 кубометра. Фактически с этого момента следует, что переплата за 1 кубометр этого популярного стройматериала может составлять 1% от реальной цены. Например, 5500 вместо 4995 руб.
Для расчета кубатуры необрезного типа доски используются несколько иные методы. Если речь идет о покупке 1 доски, то замер ее толщины, а также общей длины производится так же, как и при выборе обрезного стройматериала.В этом случае ширина для расчетов берется усредненной — между большим значением и малым.
Например, если на конце ширина доски 25 см, а на другом 20, то среднее значение будет примерно 22 сантиметра. Когда необходимо рассчитать объем значительного количества таких досок для строительства, то нужно будет расположить их так, чтобы широкая не отличалась от узкой, более 10 см. Основная длина этого материала в развернутом ворсе должна быть примерно такой же.После этого при помощи обычной рулетки измеряется точная высота всей стопки досок, и измеряется ширина (примерно посередине). Полученный результат затем необходимо умножить на специальный коэффициент от 0,07 до 0,09, прямо пропорциональный существующему воздушному зазору.
Сколько в 1 кубе досок: специальные таблицы
Для точного расчета количества досок определенной ширины, длины в 1 куб.м используются различные таблицы. Ниже приведены некоторые из этих специализированных таблиц, в которых указана кубатура типов этого материала, которые распространены и востребованы сегодня.Рассчитать объем различных досок с разными размерами, например, материала для возведения забора на своем участке, можно, используя имеющуюся формулу, которая представлена выше.
Таблица количества досок обрезных в 1 кубометре
| Размер доски | Объем 1-й доски (м 3) | Количество досок в 1 м 3 (шт.) | Количество досок квадратных метров в 1м 2 |
|---|---|---|---|
| Двадцать | |||
| Доска 20x100x6000 | 0.012 м 3 | 83 шт. | 50 м 2 |
| Доска 20x120x6000 | 0,0144 м 3 | 69 шт. | 50 м 2 |
| Доска 20x150x6000 | 0,018 м 3 | 55 шт. | 50 м 2 |
| Доска 20x180x6000 | 0,0216 м 3 | 46 шт. | 50 м 2 |
| Доска 20x200x6000 | 0,024 м 3 | 41 шт. | 50 м 2 |
| Доска 20x250x6000 | 0,03 м 3 | 33 шт. | 50 м 2 |
| Двадцать пять | |||
| Доска 25x100x6000 | 0,015 м 3 | 67 шт. | 40 м 2 |
| Доска 25x120x6000 | 0,018 м 3 | 55 шт. | 40 м 2 |
| Доска 25x150x6000 | 0,0225 м 3 | 44 шт. | 40 м 2 |
| Доска 25x180x6000 | 0,027 м 3 | 37 шт. | 40 м 2 |
| Доска 25x200x6000 | 0,03 м 3 | 33 шт. | 40 м 2 |
| Доска 25x250x6000 | 0,0375 м 3 | 26 шт. | 40 м 2 |
| Тридцать | |||
| Доска 30x100x6000 | 0,018 м 3 | 55 шт. | 33 м 2 |
| Доска 30x120x6000 | 0,0216 м 3 | 46 шт. | 33 м 2 |
| Доска 30x150x6000 | 0,027 м 3 | 37 шт. | 33 м 2 |
| Доска 30x180x6000 | 0,0324 м 3 | 30 шт. | 33 м 2 |
| Доска 30x200x6000 | 0,036 м 3 | 27 шт. | 33 м 2 |
| Доска 30x250x6000 | 0,045 м 3 | 22 шт. | 33 м 2 |
| Тридцать | |||
| Доска 32x100x6000 | 0.0192 м 3 | 52 шт. | 31 м 2 |
| Доска 32x120x6000 | 0,023 м 3 | 43 шт. | 31 м 2 |
| Доска 32x150x6000 | 0,0288 м 3 | 34 шт. | 31 м 2 |
| Доска 32x180x6000 | 0,0346 м 3 | 28 шт. | 31 м 2 |
| Доска 32x200x6000 | 0,0384 м 3 | 26 шт. | 31 м 2 |
| Доска 32x250x6000 | 0,048 м 3 | 20 шт. | 31 м 2 |
| Сорока | |||
| Доска 40x100x6000 | 0,024 м 3 | 41 шт. | 25 м 2 |
| Доска 40x120x6000 | 0,0288 м 3 | 34 шт. | 25 м 2 |
| Доска 40x150x6000 | 0,036 м 3 | 27 шт. | 25 м 2 |
| Доска 40x180x6000 | 0,0432 м 3 | 23 шт. | 25 м 2 |
| Доска 40x200x6000 | 0,048 м 3 | 20 шт. | 25 м 2 |
| Доска 40x250x6000 | 0,06 м 3 | 16 шт. | 25 м 2 |
| Пятидесятница | |||
| Доска 50x100x6000 | 0,03 м 3 | 33 шт. | 20 м 2 |
| Доска 50х120х6000 | 0,036 м 3 | 27 шт. | 20 м 2 |
| Доска 50х150х6000 | 0,045 м 3 | 22 шт. | 20 м 2 |
| Доска 50x180x6000 | 0,054 м 3 | 18 шт. | 20 м 2 |
| Доска 50x200x6000 | 0,06 м 3 | 16 шт. | 20 м 2 |
| Доска 50х250х6000 | 0,075 м 3 | 13 шт. | 20 м 2 |
Таблица количества пиломатериалов в 1 м3
| Размер балки | Объем 1-й шт. (М³) | Количество пиломатериалов в 1 м³ (шт.) |
|---|---|---|
| 100 × 100 × 6000 | 0,06 м 3 | 16 шт. |
| 100 × 150 × 6000 | 0,09 м 3 | 11 шт. |
| 150 × 150 × 6000 | 0,135 м 3 | 7 шт. |
| 100 × 180 × 6000 | 0,108 м 3 | 9 шт. |
| 150 × 180 × 6000 | 0,162 м 3 | 6 шт. |
| 180 × 180 × 6000 | 0.1944 м 3 | 5 шт. |
| 100 × 200 × 6000 | 0,12 м 3 | 8 шт. |
| 150 × 200 × 6000 | 0,18 м 3 | 5,5 шт. |
| 180 × 200 × 6000 | 0,216 м 3 | 4,5 шт. |
| 200 × 200 × 6000 | 0,24 м 3 | 4 шт. |
| 250 × 200 × 6000 | 0,3 м 3 | 3 шт. |
Таблица количества необрезных досок в 1 кубометре
Древесина является наиболее распространенным сырьем для строительных материалов, поэтому всегда существует высокий спрос на доску или брус.
Многие не знают, как посчитать, сколько этого пиломатериала на 1 кубометр? Известно, что 1 куб — это объем, длина, ширина и высота, равные 1 метру. Вы, конечно, можете использовать для расчетов онлайн-калькулятор, но в любом случае лучше выучить эту простую вещь самостоятельно.
Причины расчета вполне понятны: вы рассчитаете количество материала для покупки и определите примерную стоимость. Помните, что изделия разных производителей имеют разные габариты, поэтому внимательно изучайте (особенно ширину, длину и высоту).Например, определяем, сколько досок 50х150х6000 входит в метровый куб и рассчитываем кубатуру одной штуки.
Сколько кубиков в одной доске
Сначала рассчитайте кубатуру обрезной доски (V) в метрах. Для этого переведем длину (a), ширину (b) и высоту (c) в метры, разделив на 1000, а затем умножим эти три показателя, получим результат в кубических метрах.
- 6000мм = 6 м;
- 150 мм = 0.15 м;
- 50 мм = 0,05 м.
Формула расчета объема следующая: a *
b *
с =
В
V = 6 * 0,15 * 0,05 = 0,045 м³
Для этого делим 1 куб на кубатуру (V) 50x150x6000, получено ранее.
Формула расчета следующая: 1 /
В =
K (количество досок)
К = 1 / 0,045 = 22,22 доски
Если количество досок оказалось дробным, лучше округлить в большую сторону, то есть потребуется приобрести 23 доски.Также важно помнить, особенно при закупке крупными партиями, что не все доски хорошего качества, может попадаться брак. Поэтому во избежание недостатка материала разумно будет покупать с наценкой.
Сколько метров в одном кубе
Если вам нужно построить большую конструкцию, вам нужно будет вычислить общее количество метров в кубе.
Для этой операции нам нужно знать количество плат и кубатуру одной платы, которые мы уже нашли ранее.Делается это очень просто, достаточно умножить эти два значения.
Формула для расчета выглядит следующим образом:
К (количество досок) * V (кубатура доски) = Т (метры в кубе)
T = 22,22 * 0,045 м³ = 0,999 м³
Следует помнить, что и в этом случае будет разумнее округлить число в большую сторону.
Результаты расчетов
Подведем итоги, для большего удобства оформив все эти расчеты в табличной форме.
Измерение стоящих деревьев | Ohioline
Владельцам лесных угодий часто необходимо измерить коммерческое содержание дощатого настила (называемое «объемом») в определенных деревьях в их лесном массиве. Например, для продажи древесины требуется оценка количества, которое будет продано. Если деревья должны быть спилены для получения пиломатериалов, необходима оценка объема, чтобы определить, какого размера и сколько деревьев нужно спилить. Используя методы, описанные в этой статье, владелец лесного участка может оценить объем дощатого настила на одном или нескольких деревьях.Однако, если требуется оценка нескольких акров земли, владельцу лесного участка рекомендуется воспользоваться услугами отдела лесного хозяйства Департамента природных ресурсов штата Огайо, лесничего-консультанта или отраслевого лесничего. Методы, необходимые для точной и эффективной инвентаризации древесины на больших площадях, выходят за рамки данной публикации.
Оценка объема дерева
В Соединенных Штатах наиболее распространенной мерой объема пиломатериалов является подошва доски, определяемая как кусок дерева, содержащий 144 кубических дюйма.Его проще всего представить в виде доски размером 12 дюймов в квадрате и толщиной в один дюйм (12 дюймов x 12 дюймов x 1 дюйм = 144 кубических дюйма). Однако любой кусок дерева, содержащий 144 кубических дюйма, составляет дощатый фут (например, 3 дюйма). x 4 «x 12»; 2 «x 6» x 12 «; и т. д.). Содержание досок в футах любой доски может быть определено путем умножения длины на ширину на толщину, все выражено в дюймах, и деления на 144 кубических дюйма.
Основание доски также является наиболее распространенной мерой объема для деревьев и бревен, используемых для пиломатериалов и шпона.Объем доски в футах дерева или бревна — это выражение количества футах доски пиломатериала, которые можно вырезать из этого дерева или бревна. Объем пиломатериалов, который можно вырезать из дерева или бревна, зависит от множества переменных, включая то, как дерево распиливается на бревна, размеры пиломатериалов, сколько бревна теряется в опилках и отходах, а также эффективность лесопилки и рабочих. Из-за этих переменных объем доскового фута дерева или бревна не может быть точно измерен, но оценен.
Были разработаны многочисленные методы (так называемые «правила») для оценки объема досок. В Огайо обычно используются два правила объема доск-фут: правила Дойля и международные правила 1/4 дюйма (таблицы 1 и 2). Оба эти правила обеспечивают оценку содержания дощатого фута в дереве на основе диаметра ствола дерева по высоте грудки и высоты дерева, пригодного для продажи (обсуждается позже). Правило Дойла — наиболее распространенное правило в Огайо. Его используют в лесной промышленности и многие профессиональные лесники.Международное правило 1/4 дюйма используется государственными агентствами и Лесной службой США.
| Таблица 1. Объемы ножек стоящей деревянной доски — Правило Дойля | ||||||||
| Dbh (дюймы) | Количество 16-футовых бревен | |||||||
| 1/2 | 1 | 1-1 / 2 | 2 | 2-1 / 2 | 3 | 3-1 / 2 | 4 | |
| Ножки доски | ||||||||
| 12 | 20 | 30 | 40 | 50 | 60 | |||
| 14 | 30 | 50 | 70 | 80 | 90 | 100 | ||
| 16 | 40 | 70 | 100 | 120 | 40 | 160 | 180 | 190 |
| 18 | 60 | 100 | 130 | 160 | 200 | 220 | 40 | 160 |
| 20 | 80 | 130 | 180 | 220 | 260 | 300 | 320 | 360 |
| 22 | 100 | 170 | 230 | 280 | 340 | 380 | 420 | 460 |
| 24 | 130 | 220 | 290 | 360 | 430 | 490 | 540 | 600 |
| 26 | 160 | 260 | 360 | 440 | 520 | 590 | 660 | 740 |
| 28 | 190 | 320 | 430 | 520 | 620 | 710 | 800 | 880 |
| 30 | 230 | 380 | 510 | 630 | 740 | 840 | 940 | 1 040 |
| 32 | 270 | 440 | 590 | 730 | 860 | 990 | 1,120 | 1,220 |
| 34 | 300 | 510 | 680 | 850 | 1 000 | 1,140 | 1,300 | 1,440 |
| 36 | 350 | 580 | 780 | 970 | 1,140 | 1,310 | 1,480 | 1,640 |
| 38 | 390 | 660 | 880 | 1,100 | 1,290 | 1,480 | 1,680 | 1860 |
| 40 | 430 | 740 | 990 | 1,230 | 1,450 | 1,660 | 1880 | 2 080 |
| 42 | 470 | 830 | 1,100 | 1,370 | 1,620 | 1860 | 2 100 | 2,320 |
| Откуда: Эшли, Берл С.1980. Справочник лесников. USDA NA-FR-15. 35 с. | ||||||||
Сравнение этих двух таблиц томов покажет, что они не идентичны. Международное правило 1/4 дюйма обычно считается наилучшей оценкой количества пиломатериалов, которое может быть фактически распилено из дерева или бревна при оптимальных условиях. Правило Дойля существенно недооценивает объем деревьев в классах меньшего диаметра. Поэтому международное правило 1/4 дюйма следует использовать, когда важна наиболее точная оценка урожайности, например, при определении количества деревьев, которые нужно спилить, чтобы получить заданное количество пиломатериалов.Однако при сбыте древесины на корню выбор правила объема менее критичен. Не должно возникать путаницы в отношении количества, если и покупатель, и продавец знают, какое правило использовалось для оценки объемов. Цены на древесину на корню обычно корректируются в зависимости от того, какое правило используется.
Измерение диаметра дерева
Диаметр ствола дерева измеряется на высоте груди (называемый диаметром на высоте груди или DBH), определяемым как диаметр дерева на высоте 4½ фута над землей на верхней стороне дерева.Если дерево разветвляется ниже уровня груди, каждый ствол рассматривается как отдельное дерево. DBH можно измерить штангенциркулем для дерева, палкой Билтмора, лентой для измерения диаметра дерева или гибкой измерительной лентой (например, тканевой или стальной). Штангенциркули для деревьев, палки Biltmore и ленты для диаметра деревьев можно приобрести у компаний, поставляющих лесозаготовительное оборудование. Гибкая измерительная лента может использоваться для измерения окружности ствола дерева и деления окружности на 3,14 для определения диаметра.
| Таблица 2.Объем стопы для стоящей деревянной доски — Международное правило 1/4 дюйма | ||||||||
| Dbh (дюймы) | Количество 16-футовых бревен | |||||||
| 1/2 | 1 | 1-1 / 2 | 2 | 2-1 / 2 | 3 | 3-1 / 2 | 4 | |
| Ножки доски | ||||||||
| 12 | 30 | 60 | 80 | 100 | 120 | |||
| 14 | 40 | 80 | 110 | 140 | 160 | 180 | ||
| 16 | 60 | 100 | 150 | 180 | 210 | 250 | 280 | 310 |
| 18 | 70 | 140 | 190 | 240 | 280 | 320 | 360 | 400 |
| 20 | 90 | 170 | 240 | 300 | 350 | 400 | 450 | 500 |
| 22 | 110 | 210 | 290 | 360 | 430 | 490 | 560 | 610 |
| 24 | 130 | 250 | 350 | 430 | 510 | 590 | 660 | 740 |
| 26 | 160 | 300 | 410 | 510 | 600 | 700 | 790 | 880 |
| 28 | 190 | 350 | 480 | 600 | 700 | 810 | 920 | 1 020 |
| 30 | 220 | 410 | 550 | 690 | 810 | 930 | 1 060 | 1,180 |
| 32 | 260 | 470 | 640 | 790 | 940 | 1 080 | 1,220 | 1,360 |
| 34 | 290 | 530 | 730 | 900 | 1 060 | 1,220 | 1,380 | 1,540 |
| 36 | 330 | 600 | 820 | 1 010 | 1,200 | 1,380 | 1,560 | 1,740 |
| 38 | 370 | 670 | 910 | 1,130 | 1,340 | 1,540 | 1,740 | 1 940 |
| 40 | 420 | 740 | 1 010 | 1,250 | 1,480 | 1,700 | 1 920 | 2,160 |
| 42 | 460 | 820 | 1,100 | 1,360 | 1,610 | 1870 | 2 120 | 2,360 |
| Откуда: Эшли, Берл С.1980. Справочник лесников. USDA NA-FR-15. 35 с. | ||||||||
Измерение товарной высоты
Товарная высота — это высота дерева (или длина его ствола), до которой может быть получен конкретный продукт, обычно за вычетом высоты пня в один фут. Товарная высота пиловочника и фанеры обычно оценивается по высоте, при которой диаметр ствола сужается до 10 дюймов или до тех пор, пока не обнаружатся сильные ветвления или дефекты.Товарная высота очень ценных деревьев, таких как шпон черного ореха, может измеряться с точностью до фута или двух футов. Торговая высота большинства других деревьев измеряется в единицах 16-футовых бревен и 8-футовых полубревен. Товарные размеры округлены до ближайшего полбревна. Таким образом, дерево с коммерческой высотой 42 фута будет измерено как имеющее 2½ бревна коммерческой высоты.
Товарная высота может быть измерена с помощью ряда специальных инструментов, разработанных специально для измерения высоты деревьев, таких как клинометры, высотомеры, ретоскопы или гипсометры.Эти инструменты можно приобрести у компаний-поставщиков лесозаготовительного оборудования. Товарную высоту также можно измерить с помощью длинного шеста, если измеряется только несколько деревьев и они имеют относительно небольшую товарную высоту. С некоторой практикой товарная высота в единицах бревна и полубревна может быть оценена довольно точно, особенно для деревьев с небольшой коммерческой высотой.
Использование таблиц для оценки объема товарного дерева
После измерения диаметра на высоте груди и коммерческой высоты дерева можно использовать Таблицу 1 или 2 для оценки его объема в футах доски.Например, 20-дюймовый дуб DBH с коммерческой высотой 2½ бревна содержит 260 футов доски по правилу Дойля или 350 футов по международному правилу 1/4 дюйма.
При использовании этих таблиц важно помнить, что следует измерять только ту часть ствола, которая будет производить полезный продукт. Части ствола или целые стволы полые, чрезмерно искривленные, гнилые и т. Д. Не подлежат измерению. Вы можете услышать, как лесники или покупатели говорят о валовом и чистом объеме. Общий объем — это расчетный объем дерева без вычета дефектов (т.е., DBH и коммерческая высота всех деревьев были измерены без учета дефектов, объемы были определены, и объемы были суммированы). Чистый объем — это предполагаемый объем дерева с соответствующими вычетами по дефектам.
Mathematics_ _solutions for Class 8 Math Глава 2
Страница № 30:
Вопрос 1:
Выразите математически следующие утверждения:
(i) квадрат из 4 равно 6; (ii) квадрат 8 равно 64; (iii) квадрат из 15 равен 225.
Ответ:
(i) 4 2 = 16
(ii) 8 2 = 64
(iii) 15 2 = 225
Страница № 30:
Вопрос 2:
Найдите квадраты префектов среди следующих чисел;
1, 2, 3, 8, 36, 49, 65, 67, 71, 81, 169, 625, 125, 900, 100, 1000, 100000.
Ответ:
6 2 = 36
7 2 = 49
9 2 = 81
13 2 = 169
25 2 = 625
30 2 = 900
10 2 = 100
Следовательно, 36, 49, 81, 169, 625, 900 и 100 — полные квадраты.
Страница № 30:
Вопрос 3:
Составьте список всех идеальных квадратов от 1 до 500.
Ответ:
1 2 = 1
2 2 = 4
3 2 = 9
4 2 = 16
5 2 = 25
6 2 = 36
7 2 = 49
8 2 = 64
9 2 = 81
10 2 = 100
11 2 = 121
12 2 = 144
13 2 = 169
14 2 = 196
15 2 = 225
16 2 = 256
17 2 = 289
18 2 = 324
19 2 = 361
20 2 = 400
21 2 = 441
22 2 = 484
Следовательно, идеальные квадраты от 1 до 500 равны 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400. , 441 и 484.
Страница № 30:
Вопрос 4:
Запишите трехзначные числа, оканчивающиеся на 0, 1, 4, 5, 6, 9, по одному на каждую цифру, но ни одно из них не является полным квадратом.
Ответ:
Цифры: 100, 101, 104, 105, 106 и 109.
Есть и другие возможности, например 110, 111, 124, 115, 116 и 119.
Страница № 30:
Вопрос 5:
Найдите числа от 100 до 400, оканчивающиеся на 0, 1, 4, 5, 6 или 9, которые являются точными квадратами.
Ответ:
10 2 = 100
11 2 = 121
12 2 = 144
13 2 = 169
14 2 = 196
15 2 = 225
16 2 = 256
17 2 = 289
18 2 = 324
19 2 = 361
20 2 = 400
Следовательно, требуемые числа: 100, 121, 144, 169, 196, 225, 256, 289, 324, 361 и 400.
Страница № 34:
Вопрос 1:
Найдите сумму 1 + 3 + 5 +… + 51 (сумму всех нечетных чисел от 1 до 51), не складывая их.
Ответ:
Здесь частное, полученное при делении 51 на 2, равно 25.
∴Количество терминов = n = 25 + 1 = 26
∴ 1 + 3 + 5 +… + 51 = 26 2 = 676
Страница № 34:
Вопрос 2:
Выразите 144 как сумму 12 нечетных чисел.
Ответ:
Здесь n = 12
Сейчас, 1 + 3 + 5 +… + 23 = 12 2 = 144
Таким образом, сумма первых 12 нечетных чисел 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и 23 равна 144.
Страница № 34:
Вопрос 3:
Найдите 14-е и 15-е треугольные числа и найдите их сумму. Проверьте эту сумму в выписке 8 .
Ответ:
Треугольные числа 14 и 15 :
14 -е треугольное число = 1 + 2 + 3 + 4 +… + 14 = 105
15 -е треугольное число = 1 + 2 + 3 + 4 +… + 14 + 15 = 120
Сумма треугольных чисел 14 и 15 = (14 + 1) 2 = 225
Здесь 105 + 120 = 225
Следовательно, утверждение 8 проверено.
Страница № 34:
Вопрос 4:
Каковы остатки идеального квадрата при делении на 5?
Ответ:
Совершенное число всегда заканчивается одной из цифр 0, 1, 4, 5, 6 и 9.
Следовательно, когда идеальное число делится на 5, остаток будет равен 0, 1, 4, 0, 1 или 4. [5 — 5 = 0, 6 — 5 = 1, 9 — 5 = 4]
Следовательно, возможные остатки равны 0, 1 и 4.
Стр. № 35:
Вопрос 1:
Найдите квадраты:
(i) 31, (ii) 72; (iii) 37; (iv) 166.
Ответ:
(i) ( a + b ) 2 = a 2 + 2 ab + b 2
∴31 2 = (30 + 1) 2 = 30 2 + 2 × 30 × 1 + 1 2 = 900 + 60 + 1 = 961
(ii) ( a + b ) 2 = a 2 + 2 ab + b 2
∴72 2 = (70 + 2) 2 = 4900 + 280 + 4 = 5184
(iii) ( a + b ) 2 = a 2 + 2 ab + b 2
∴37 2 = (30 + 7) 2 = 900 + 420 + 49 = 1369
(iv) ( a + b ) 2 = a 2 + 2 ab + b 2
∴166 2 = (160 + 6) 2 = 25600 + 1920 + 36 = 27556
Стр. № 35:
Вопрос 2:
Найдите квадраты; (i) 85; (ii) 115; (iii) 165.
Ответ:
(i) 85 оканчивается на 5.
Сейчас, 8 × (8 + 1) = 72
∴ 85 2 = 7225
(ii) 115 оканчивается на 5.
Сейчас, 11 × (11 + 1) = 132
∴ 115 2 = 13225
(iii) 165 оканчивается на 5.
Сейчас, 16 × (16 + 1) = 272
∴ 165 2 = 27225
Стр. № 35:
Вопрос 3:
Найдите квадрат 1468, записав это как 1465 + 3.
Ответ:
( a + b ) 2 = a 2 + 2 ab + b 2
∴1468 2 = (1465 + 3) 2 = 1465 2 + 2 × 1465 × 3 + 9 = 1465 2 + 8799
Число 1465 заканчивается на 5.
Сейчас, 146 × (146 + 1) = 21462
∴ 1465 2 = 2146225
∴ 1468 2 = 2146225 + 8799 = 2155024
Стр. № 40:
Вопрос 1:
Найдите квадратный корень из следующих чисел путем факторизации:
(i) 196; (ii) 256; (iii) 10404; (iv) 1156; (в) 13225.
Ответ:
(i) 196 = 2 × 7 × 2 × 7 = (2 × 7) × (2 × 7)
∴
(ii) 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = (2 × 2 × 2 × 2) × (2 × 2 × 2 × 2)
∴
(iii) 10404 = 2 × 2 × 3 × 3 × 17 × 17 = (2 × 3 × 17) × (2 × 3 × 17)
∴
(iv) 1156 = 2 × 2 × 17 × 17 = (2 × 17) × (2 × 17)
∴
(v) 13225 = 5 × 5 × 23 × 23 = (5 × 23) × (5 × 23)
∴
Стр. № 41:
Вопрос 2:
Упростить:
(i) ;
(ii) ;
(iii) ;
(iv)
(v) ;
(vi) .
Ответ:
(i)
(ii)
(iii)
(iv)
(в)
(vi)
Стр. № 41:
Вопрос 3:
Квадратный двор площадью 1764 м 2 .Из угла этого двора в коммунальные услуги отведена другая квадратная часть площадью 784 м 2 . Оставшаяся часть делится на 5 равных квадратных частей. Каков периметр каждой из этих равных частей?
Ответ:
Площадь оставшейся части = 1764 — 784 = 980 м 2
∴ Площадь одной части из 5 равных частей = (980 ÷ 5) м 2 = 196
Сторона квадрата площадью 196 м 2 =
∴Периметр каждой квадратной части = (14 + 14 + 14 + 14) м = 56 м
Стр. № 41:
Вопрос 4:
Найдите наименьшее положительное целое число, на которое нужно умножить каждое из следующих чисел, чтобы получить полный квадрат:
(i) 847; (ii) 450; (iii) 1445; (iv) 1352.
Ответ:
(i) 847 = 7 × 11 × 11
847 × 7 = 7 × 7 × 11 × 11
Следовательно, требуется целое число 7.
(ii) 450 = 2 × 3 × 3 × 5 × 5
450 × 2 = 2 × 2 × 3 × 3 × 5 × 5
Следовательно, требуется целое число 2.
(iii) 1445 = 5 × 17 × 17
1445 × 5 = 5 × 5 × 17 × 17
Следовательно, требуется целое число 5.
(iv) 1352 = 2 × 2 × 2 × 13 × 13
1352 × 2 = 2 × 2 × 2 × 2 × 13 × 13
Следовательно, требуется целое число 2.
Стр. № 41:
Вопрос 5:
Найдите наибольший коэффициент полного квадрата каждого из следующих чисел:
(i) 48; (ii) 11280; (iii) 729; (iv) 1352.
Ответ:
(i) 48 = 3 × 4 × 4
4 × 4 = 16
Следовательно, наибольший коэффициент квадрата 48 равен 16.
(ii) 11280 = 2 × 2 × 2 × 2 × 5 × 141
2 × 2 × 2 × 2 = 16
Следовательно, наибольший квадратный коэффициент 11280 равен 16.
(iii) 729 = 3 × 3 × 3 × 3 × 3 × 3
Следовательно, наибольший квадратный множитель 729 равен самому 729.
(iv) 1352 = 2 × 2 × 2 × 13 × 13
2 × 2 × 13 × 13 = 676
Следовательно, наибольший коэффициент полного квадрата 1352 равен 676.
Стр. № 41:
Вопрос 6:
Найдите правильный положительный множитель 48 и положительное кратное 48, которые в сумме дают полный квадрат. Можете ли вы доказать, что таких пар бесконечно много?
Ответ:
Возьмем 16 как множитель 48 и 48 k как множитель 48.
Пусть k = n (3 n + 2), n = 1, 2, 3…
Следовательно, таких пар бесконечно много.
Стр. № 43:
Вопрос 1:
Найдите ближайшее целое число к квадратному корню из следующих чисел:
(i) 232; (ii) 600; (iii) 728; (iv) 824; (в) 1729.
Ответ:
(i) 15 2 = 225 <232 <16 2 = 256
Здесь 232 ближе к 225.
Следовательно, ближайшее целое число равно 15.
(ii) 24 2 = 576 <600 <25 2 = 625
Здесь 600 ближе к 576.
Следовательно, ближайшее целое число равно 24.
(iii) 26 2 = 676 <728 <27 2 = 729
Здесь 728 ближе к 729.
Следовательно, ближайшее целое число равно 27.
(iv) 28 2 = 784 <824 <29 2 = 841
Здесь 824 ближе к 841.
Следовательно, ближайшее целое число к 29.
(в) 41 2 = 1691 <1729 <42 2 = 1764
Здесь 1729 год приближается к 1764 году.
Следовательно, ближайшее целое число to равно 42.
Стр. № 43:
Вопрос 2:
Участок земли в форме квадрата, площадью 1000 м 2 2 .Это должно быть ограждено колючей проволокой. Колючая проволока доступна только целой длины. Какую минимальную длину колючей проволоки нужно покупать для этой цели?
Ответ:
Пусть L будет периметром квадратной земли.
Сейчас,
126 2 = 15876 <16000 <127 2 = 16129
Здесь 16000 ближе к 16129.
Следовательно, минимальная длина провода 127 м.
Стр. № 43:
Вопрос 3:
Студента попросили найти. Он прочитал это неправильно и нашел до ближайшего целого числа. Насколько мал был его номер от правильного ответа?
Ответ:
Сейчас, 26 2 = 676 <691 <27 2 = 729
Здесь 691 ближе к 676.
Таким образом, ближайшее целое число равно 26.
Разница = 31 — 26 = 5
Таким образом, его число было меньше правильного ответа на 5.
Стр. № 45:
Вопрос 1:
Глядя на узор, заполните следующие пробелы;
2 | 3 | 4 | — 5 | 6 | 8 | –9 |
2 3 = 8 | 3 3 = __ | __ = 64 | __ = __ | 6 3 = __ | __ = __ | __ = –729 |
Ответ:
2 | 3 | 4 | — 5 | 6 | 8 | –9 |
2 3 = 8 | 3 3 = 27 | 4 3 = 64 | (–5) 3 = –125 | 6 3 = 216 | 8 3 = 512 | (–9) 3 = –729 |
Стр. № 45:
Вопрос 2:
Найдите кубики первых пяти нечетных натуральных чисел и кубы первых пяти четных натуральных чисел.Что вы можете сказать о четности кубиков нечетных и четных?
Ответ:
1 3 | 3 3 | 5 3 | 7 3 | 9 3 | 2 3 | 4 3 | 6 3 | 8 3 | 10 3 |
1 | 27 | 125 | 343 | 729 | 8 | 64 | 216 | 512 | 1000 |
Куб нечетного числа является нечетным, а куб четного числа — четным.
Стр. № 45:
Вопрос 3:
Сколько идеальных кубиков вы можете найти от 1 до 100? Сколько от −100 до 100?
Ответ:
1 3 = 1
2 3 = 8
3 3 = 27
4 3 = 64
Таким образом получается 4 куба от 1 до 100.
Сейчас, 0 3 = 0
(-1) 3 = -1
(−2) 3 = −8
(−3) 3 = −27
(−4) 3 = −64
Следовательно, есть 9 кубов от −100 до 100.
Стр. № 45:
Вопрос 4:
Сколько существует идеальных кубиков от 1 до 500? Сколько среди этих кубиков совершенных квадратов?
Ответ:
1 3 = 1
2 3 = 8
3 3 = 27
4 3 = 64 = 8 2
5 3 = 125
6 3 = 216
7 3 = 343
8 3 = 512
Таким образом, есть 7 совершенных кубов от 1 до 500, и 64 — единственный правильный квадрат.
Стр. № 45:
Вопрос 5:
Найдите кубики 10, 30, 100, 1000. Что вы можете сказать о нулях в конце?
Ответ:
10 3 = 1000
30 3 = 27000
100 3 = 1000000
1000 3 = 1000000000
Число нулей в конце всегда кратно 3.
Стр. № 45:
Вопрос 6:
Какие цифры заменяют единицы кубиков 1, 2, 3, 4, 5, 6, 7, 8, 9, 10? Можно ли сказать, что число не является идеальным кубом, глядя на цифру вместо единицы данного числа, как вы это делали с квадратами?
Ответ:
1 3 = 1
2 3 = 8
3 3 = 2 7
4 3 = 6 4
5 3 = 12 5
6 3 = 21 6
7 3 = 34 3
8 3 = 51 2
9 3 = 72 9
10 3 = 100 0
Цифры на месте единиц: 1, 8, 7, 4, 5, 6, 3, 2 и 9.
Каждая цифра находится в конце некоторого куба.
Следовательно, нельзя заключить, что число не является идеальным кубом, глядя на его единичную цифру.
Стр. № 49:
Вопрос 1:
Найдите кубический корень путем разложения на простые множители:
(i) 10648; (ii) 46656; (iii) 15625.
Ответ:
(i) 10648
= 2 × 5324
= 2 × 2 × 2662
= 2 × 2 × 2 × 1331
= 2 × 2 × 2 × 11 × 121
= 2 × 2 × 2 × 11 × 11 × 11
∴
(ii) 46656
= 2 × 23328
= 2 × 2 × 11664
= 2 × 2 × 2 × 5832
= 2 × 2 × 2 × 2 × 2916
= 2 × 2 × 2 × 2 × 2 × 1458
= 2 × 2 × 2 × 2 × 2 × 2 × 729
= 2 × 2 × 2 × 2 × 2 × 2 × 3 × 243
= 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 3 × 3 × 3
∴
(iii) 15625
= 5 × 3125
= 5 × 5 × 625
= 5 × 5 × 5 × 5 × 5 × 5
∴
Стр. № 49:
Вопрос 2:
Найдите кубический корень из следующего, посмотрев на последнюю цифру и используя оценку:
(i)
Ответ:
(i) Пусть n 3 =
Здесь количество цифр 5; следовательно, цифра единиц n должна быть 5.
Разобьем число
Сейчас, 4 3 <91 <5 3 = 125
∴ 40 3 = 64000 < <50 3 = 125000
Поскольку цифра единиц n равна 5, единственное возможное число — 45.
Можно проверить, что
(ii) Пусть n 3 = 166375
Здесь количество цифр 5; следовательно, цифра единиц n должна быть 5.
Разобьем число 166375 на 166 и 375.
Сейчас, 5 3 = 125 <166 <6 3 = 216
∴ 50 3 = 125000 <166000 <60 3 = 216000
Поскольку цифра единиц n равна 5, единственное возможное число — 55.
Можно проверить, что
(iii) Пусть n 3 = 704969.
Здесь единицы измерения — 9; следовательно, цифра единиц n должна быть 9.
Разобьем число 704969 на 704 и 969.
Сейчас 8 3 = 512 <704 <9 3 = 729
∴ 80 3 = 512000 <704000 <90 3 = 729000
Поскольку цифра единиц n равна 9, единственное возможное число — 89.
Можно проверить, что
Стр. № 49:
Вопрос 3:
Найдите ближайшее целое число к кубическому корню каждого из следующих чисел:
(i) 331776; (ii) 46656; (iii) 373248.
Ответ:
(i) 331776
Мы видим, что 6 3 = 216 <331 <7 3 = 343
∴ 60 3 = 216000 <331000 <70 3 = 343000
Сейчас, 69 3 = 328509
Следовательно, должно находиться в диапазоне от 69 до 70.
Более того, 331776 ближе к 328509, чем к 343000.
Следовательно, ближайшее целое число к 69.
(ii) 46656
Мы видим, что 3 3 = 27 <46 <4 3 = 64
∴ 30 3 = 27000 <46000 <40 3 = 64000
Сейчас, 31 3 = 29791, 32 3 = 32768, 35 3 = 42875, 36 3 = 46656
∴
(iii) 373248
Мы видим, что 7 3 = 343 <373 <8 3 = 512
∴ 70 3 = 343000 <373000 <80 3 = 512000
Сейчас, 71 3 = 357911, 72 3 = 373248
∴
Страница № 50:
Вопрос 1:
Сопоставьте числа в столбце A с их квадратами в столбце B:
А | Б | Ответ | |||
_____ | _____ | ____ | |||
(1) | 5 | (а) | 25 | (1) _____ | |
(2) | 8 | (б) | 144 | (2) _____ | |
(3) | 2 | (в) | 36 | (3) _____ | |
(4) | –6 | (г) | 484 | (4) _____ | |
(5) | –22 | (д) | 64 | (5) _____ | |
(6) | 12 | (ж) | 4 | (6) _____ | |
(г) | 121 | ||||
Ответ:
5 2 = 25
8 2 = 64
2 2 = 4
(−6) 2 = 36
(-22) 2 = 484
12 2 = 144
Следовательно, (1) ↔ (a), (2) ↔ (e), (3) ↔ (f), (4) ↔ (c), (5) ↔ (d) и (6) ↔ (b)
Страница № 50:
Вопрос 2.А:
Количество полных квадратов от 1 до 500:
А. 1
Б. 16
К. 22
Д. 25
Ответ:
22 2 = 484 и 23 2 = 529
Следовательно, количество полных квадратов от 1 до 500 равно 22.
Следовательно, правильный ответ — C.
Страница № 50:
Вопрос 2.А:
Последняя цифра полного квадрата никогда не может быть
А. 1
Б. 3
К. 5
Д. 9
Ответ:
Идеальный квадрат не может заканчиваться на 3.
Следовательно, правильный ответ — B.
Страница № 50:
Вопрос 2.C:
Если число заканчивается пятью нулями, его квадрат заканчивается на:
А. 5 нулей
Б. 8 нулей
C. 10 нулей
D. 12 нулей
Ответ:
200000 2 = 40000000000
Таким образом, квадрат числа, заканчивающегося 5 нулями, оканчивается 10 нулями.
Следовательно, правильный ответ — C.
Страница № 50:
Вопрос 2.D:
Какой может быть остаток из следующего, когда полный квадрат делится на 8?
А. 1
Б. 3
К. 5
Д. 7
Ответ:
Рассмотрим число 3.
3 2 = 9 и остаток, полученный при делении 9 на 8, равен 1.
Следовательно, правильный ответ — А.
Страница № 50:
Вопрос 2.E:
Шестое треугольное число:
А. 6
Б. 10
К. 21
Д. 28
Ответ:
Шестое треугольное число: 1 + 2 + 3 + 4 + 5 + 6 = 21
Следовательно, правильный ответ — C.
Страница № 50:
Вопрос 3:
Возьмите все целые числа от −10 до 5 и возведите каждое из них в квадрат. Сколько у вас различных чисел?
Ответ:
(-10) 2 = 100
(−9) 2 = 81
(-8) 2 = 64
(−7) 2 = 49
(−6) 2 = 36
(−5) 2 = 25
(−4) 2 = 16
(−3) 2 = 9
(-2) 2 = 4
(-1) 2 = 1
0 2 = 0
1 2 = 1
2 2 = 4
3 2 = 9
4 2 = 16
5 2 = 25
Замечено, что существует 11 различных чисел.
Страница № 50:
Вопрос 4:
Запишите цифру вместо единицы, когда возведут в квадрат следующие числа:
4, 5, 9, 24, 17, 76, 34, 52, 33, 2319, 18, 3458, 3453.
Ответ:
Цифры на месте квадратов чисел 4, 5, 9, 24, 17, 76, 34, 52, 33, 2319, 18, 3458 и 3453 равны 6, 5, 1, 6, 9, 6, 6, 4, 9, 1, 4, 4 и 9
Причина: 4 × 4 = 1 6 , 5 × 5 = 2 5 и т. Д.
Стр. № 51:
Вопрос 5:
Напишите все числа от 400 до 425, оканчивающиеся на 2, 3, 7 или 8. Проверьте, является ли какое-либо из них полным квадратом.
Ответ:
402, 403, 407, 408, 412, 413, 417, 418, 422, 423
Мы знаем, что квадрат числа не заканчивается на 2, 3, 7 или 8.
Следовательно, ни один из них не является полным квадратом.
Стр. № 51:
Вопрос 6:
Найдите сумму цифр (111111111) 2 .
Ответ:
(111111111) 2 = 12345678987654321
∴Сумма цифр (111111111) 2 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 81
Стр. № 51:
Вопрос 7:
Предположим, x 2 + y 2 = z 2 .
(i) , если x = 4 и y = 3, найти z ;
(ii) , если x = 5 и z = 13, найти y ;
(iii) , если y = 15 и z = 17, найти x .
Ответ:
(i)
z = ± 5
(ii)
(iii)
Стр. № 51:
Вопрос 8:
Сумма из 2304 рупий поровну распределяется между несколькими людьми.Каждый получает столько рупий, сколько количество человек. Сколько получает каждый?
Ответ:
Пусть количество человек будет n .
Тогда n 2 = 2304
Следовательно, каждый человек получит рупий. 48.
Стр. № 51:
Вопрос 9:
Определите новую операцию * для набора всех натуральных чисел как m * n = m 2 + n 2 .
(i) N закрыт под *?
(ii) Является ли * коммутативным на N?
(iii) Является ли * ассоциативным по N?
(iv) Есть ли в N элемент идентичности относительно *?
Ответ:
(i) Поскольку сумма квадратов положительных целых чисел является положительным целым числом, N закрывается символом *.
(ii)
Таким образом, операция * коммутативна на N .
(iii) Так как,
Таким образом, операция * ассоциативна на N .
(iv) Рассмотрим.
Это возможно только при k = 0.
Однако 0 не является натуральным числом.
Следовательно, в N нет идентификационного элемента в отношении *.
Стр. № 51:
Вопрос 10:
(Исследование) Найдите все полные квадраты от 1 до 500, каждый из которых является суммой двух полных квадратов.
Ответ:
Можно заметить, что:
5 2 = 3 2 + 4 2 [25 = 9 + 16]
10 2 = 6 2 + 8 2 [100 = 36 + 64]
13 2 = 5 2 + 12 2 [169 = 25 + 144]
17 2 = 8 2 + 15 2 [289 = 64 + 225]
Таким образом, требуются полные квадраты 25, 100, 169 и 289.
Стр. № 51:
Вопрос 11:
Предположим, что площадь квадратного поля составляет 7396 м 2 . Найдите его периметр.
Ответ:
Площадь квадрата = сторона × сторона
⇒ Сторона =
∴ Периметр квадрата = 4 × Сторона = 4 × 86 м = 344 м
Стр. № 51:
Вопрос 12:
Можно ли 1010 записать как разность двух полных квадратов? [Подсказка: сколько раз 2 встречается в 1010 раз?]
Ответ:
Предположим
Поскольку 1010 является четным, и x , и y либо четные, либо нечетные.
Следовательно, делится на 4.
Однако 1010 не делится на 4, так как 10 не делится на 4.
Следовательно, 1010 нельзя записать как разность двух полных квадратов.
Стр. № 51:
Вопрос 13:
Каковы остатки от деления идеального куба на 7?
Ответ:
1 3 ÷ 7 = 1
2 3 ÷ 7 = 1
3 3 ÷ 7 = 6
4 3 ÷ 7 = 1
5 3 ÷ 7 = 6
6 3 ÷ 7 = 6
7 3 ÷ 7 = 0
8 3 ÷ 7 = 1
9 3 ÷ 7 = 1
Можно заметить, что когда идеальный куб делится на 7, остатки равны 0, 1 или 6.
Стр. № 51:
Вопрос 14:
Какой наименьший идеальный квадрат дает остаток 1 при делении как на 7, так и на 11?
Ответ:
Пусть требуемый наименьший идеальный квадрат равен x 2 .
Тогда по данному условию ( x 2 — 1) делится на 7 и 11.
⇒ ( x 2 — 1) делится на 77 [77 = 7 × 11]
Кратное 77: 77, 154, 231, 308, 385, 462, 539, 616, 693, 770, 847, 924, 1001, 1078, 1155, 1232…
Рассмотрим числа 78, 155, 232, 309, 386, 463, 540, 617, 694, 771, 848, 925, 1002, 1079, 1156, 1233…
Среди этих чисел можно заметить, что 1156 (= 34 2 ) — это первый полный квадрат.
Следовательно, 1156 — это требуемый наименьший идеальный квадрат.
Стр. № 51:
Вопрос 15:
Найдите два наименьших совершенных квадрата, произведение которых представляет собой идеальный куб.
Ответ:
Список идеальных кубиков приведен ниже.
1 = 1 × 1 × 1
8 = 2 × 2 × 2
27 = 3 × 3 × 3
Видно, что 64 = 4 × 16.
Здесь 4 и 16 — полные квадраты.
Таким образом, требуемые наименьшие полные квадраты, произведение которых представляет собой идеальный куб, равны 4 и 16.
Просмотреть решения NCERT для всех глав класса 8
Калькулятор фанеры — оценка необходимости 4×8 листов фанеры
Оцените количество листов фанеры 4 × 8, необходимых для отделки стен, полов и потолков.
Сколько листов фанеры 4 × 8 вам нужно
Определение количества листов фанеры, необходимого для пола, стены, потолка или шкафа, начинается с определения площади, которую необходимо покрыть.Площадь можно найти, умножив длину и ширину пространства в футах. Найдите квадратные метры каждого помещения и сложите их, чтобы найти общий необходимый квадратный метр.
Разделите общую площадь в квадратных футах на квадратные метры листа фанеры, чтобы найти количество листов, необходимое для покрытия пространства. Лист фанеры 4 × 8 составляет 32 фута 2 .
Например, если площадь, покрываемая фанерой, составляет 800 футов 2 , то для ее покрытия потребуется 25 листов фанеры.
800 ÷ 32 = 25 листов
Получите бесплатную оценку проекта
Найдите квалифицированных плотников в вашем районе
Заказ дополнительных листов фанеры позволит избавиться от проектных отходов и лома, которые нельзя будет использовать.
Распространенные виды фанеры
Многослойный
Фанера на самом деле состоит из нескольких слоев дерева, склеенных вместе. Фанера обычно состоит из 3 или 5 слоев.
OSB
Ориентированно-стружечная плита (OSB) состоит из древесных волокон или стружек, сжатых с помощью клея.OSB обычно используется для обрамления крыш, полов и стен.
МДФ
Древесноволокнистая плита средней плотности (МДФ) состоит из небольших древесных волокон, сжатых с помощью клея. Более мелкие волокна обеспечивают аккуратные края и гладкую поверхность. МДФ обычно используется в мебельной промышленности.
ДСП
ДСП состоит из мелких древесных частиц, спрессованных с помощью клея. Частицы больше, чем волокна, используемые в МДФ, но меньше, чем хлопья, используемые в OSB. ДСП часто используют для обшивки пола, стеллажей и мебели.
Блок платы
Блочная доска — это панель, состоящая из досок, приклеенных кромкой к краю, а затем зажатых между листами шпона. Он очень прочный и жесткий и часто используется в мебели.
Толщина фанеры
Фанера часто продается толщиной 1/4 дюйма, 1/2 дюйма и 3/4 дюйма, хотя доступны и другие размеры. Необходимая толщина будет зависеть от цели и сценария использования. Более толстые панели более жесткие и долговечные, но при этом они тяжелее и дороже.Имейте в виду, что фактическая толщина фанеры часто немного меньше номинальной. Узнайте больше о фактической толщине фанеры. В большинстве случаев это не будет проблемой, но это важно иметь в виду для проектов, требующих большей точности, таких как прекрасные столярные изделия.
MEAN WELL Производитель импульсных источников питания
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
РС-15
РС-15-3.3
РС-15-5
РС-15-12
РС-15-15
РС-15-24
РС-15-48
Решение проблем | Математика для гуманитарных наук
На предыдущих курсах математики вы, несомненно, сталкивались с печально известными «проблемами со словами».«К сожалению, эти проблемы редко напоминают проблемы, с которыми мы действительно сталкиваемся в повседневной жизни. В учебниках по математике вам обычно говорят, какую именно формулу или процедуру использовать, и дают именно ту информацию, которая вам нужна, чтобы ответить на вопрос. В реальной жизни решение проблемы требует определения подходящей формулы или процедуры и определения того, какая информация вам понадобится (и не понадобится) для ответа на вопрос.
В этой главе мы рассмотрим несколько основных, но мощных алгебраических идей: проценты, ставки и пропорции.Затем мы сосредоточимся на процессе решения проблем и исследуем, как использовать эти идеи для решения проблем, для которых у нас нет точной информации.
процентов
В ходе дебатов на выборах вице-президента в 2004 году Эдвардс заявил, что американские войска понесли «90% потерь коалиции» в Ираке. Чейни оспорил это, заявив, что на самом деле иракские силы безопасности и союзники по коалиции «понесли почти 50 процентов» жертв. Кто прав? Как мы можем понять эти цифры?
Процент буквально означает «на 100» или «части на сотню».«Когда мы пишем 40%, это эквивалентно дроби [latex] \ displaystyle \ frac {40} {100} \\ [/ latex] или десятичной дроби 0,40. Обратите внимание, что 80 из 200 и 10 из 25 также составляют 40%, поскольку [latex] \ displaystyle \ frac {80} {200} = \ frac {10} {25} = \ frac {40} {100} \\ [/латекс].
Пример 1
243 человека из 400 заявили, что им нравятся собаки. Какой это процент?
Решение
[латекс] \ displaystyle \ frac {243} {400} = 0,6075 = \ frac {60,75} {100} \\ [/ latex]. Это 60,75%.
Обратите внимание, что процент можно найти, используя эквивалентную десятичную дробь, переместив десятичную запятую на два разряда вправо.
Пример 2
Запишите каждое в процентах:
- [латекс] \ displaystyle \ frac {1} {4} \\ [/ latex]
- 0,02
- 2,35
Решения
- [латекс] \ displaystyle \ frac {1} {4} = 0,25 \\ [/ latex] = 25%
- 0,02 = 2%
- 2,35 = 235%
процентов
Если у нас есть часть , которая составляет примерно процентов от целого , тогда [latex] \ displaystyle \ text {percent} = \ frac {\ text {part}} {\ text {whole}} \\ [/ latex] или, что эквивалентно, [latex] \ text {part} \ cdot \ text {whole} = \ text {percent} \\ [/ latex].
Для вычислений мы записываем процент в виде десятичной дроби.
Пример 3
Налог с продаж в городе — 9,4%. Какой налог вы заплатите при покупке за 140 долларов?
Решение
Здесь 140 долларов — это целое, и мы хотим найти 9,4% из 140 долларов. Мы начинаем с записи процента в виде десятичной дроби, перемещая десятичную запятую на два разряда влево (что эквивалентно делению на 100). Затем мы можем вычислить: налог = 0,094 (140) = 13,16 доллара США в виде налога.
Пример 4
В новостях говорится: «Ожидается, что в следующем году плата за обучение вырастет на 7%.«Если в этом году плата за обучение составляла 1200 долларов в квартал, что будет в следующем году?
Решение
Стоимость обучения в следующем году будет равна текущей стоимости обучения плюс дополнительные 7%, так что это будет 107% от стоимости обучения в этом году: 1200 долларов (1,07) = 1284 доллара.
В качестве альтернативы мы могли бы сначала вычислить 7% от 1200 долларов: 1200 долларов (0,07) = 84 доллара.
Обратите внимание, что это , а не ожидаемая плата за обучение в следующем году (мы могли только пожелать). Вместо этого это ожидаемое увеличение на , поэтому для расчета ожидаемой платы за обучение нам нужно добавить это изменение к стоимости обучения в предыдущем году: 1200 долларов США + 84 доллара США = 1284 доллара США.
Попробовать
Телевизор с первоначальной ценой 799 долларов продается со скидкой 30%. Затем взимается налог с продаж в размере 9,2%. Найдите цену с учетом скидки и налога с продаж.
Пример 5
Стоимость автомобиля упала с 7400 до 6800 долларов за последний год. На какой процент это снижение?
Решение
Чтобы вычислить процентное изменение, нам сначала нужно найти изменение стоимости в долларах: 6800 долларов — 7400 долларов = — 600 долларов. Часто мы берем абсолютное значение этой суммы, которое называется абсолютным изменением : | –600 | = 600.
Поскольку мы вычисляем уменьшение относительно начального значения, мы вычисляем этот процент из 7400 долларов:
[латекс] \ displaystyle \ frac {600} {7400} = 0,081 = [/ latex] уменьшение на 8,1%. Это называется относительным изменением .
Абсолютное и относительное изменение
Учитывая две величины,
Абсолютное изменение = [латекс] \ displaystyle | \ text {конечное количество} — \ text {начальное количество} | [/ latex]
Относительное изменение: [latex] \ displaystyle \ frac {\ text {absolute change}} {\ text {начальное количество}} [/ latex]
Абсолютное изменение имеет те же единицы, что и исходное количество.
Относительное изменение дает изменение в процентах.
Начальная величина называется базой процентного изменения.
База процента очень важна. Например, в то время как Никсон был президентом, утверждалось, что марихуана была «входным» наркотиком, утверждая, что 80% курильщиков марихуаны продолжали употреблять более тяжелые наркотики, такие как кокаин. Проблема в том, что это неправда. Истинное утверждение состоит в том, что 80% более сильных наркоманов сначала курили марихуану. Разница одна из базовых: 80% курильщиков марихуаны употребляют тяжелые наркотики, vs.80% наркоманов курили марихуану. Эти числа не эквивалентны. Как оказалось, только один из 2400 потребителей марихуаны действительно продолжает употреблять более сильные наркотики.
Пример 6
В США около 75 супермаркетов QFC. У Albertsons около 215 магазинов. Сравните размер двух компаний.
Решение
Когда мы проводим сравнения, мы должны сначала спросить, является ли сравнение абсолютным или относительным. Абсолютная разница 215 — 75 = 140.Исходя из этого, мы можем сказать: «У Albertsons на 140 магазинов больше, чем у QFC». Однако, если вы написали об этом в статье или статье, это число не имеет большого значения. Относительная разница может быть более значимой. Мы можем рассчитать два различных относительных изменения в зависимости от того, какой магазин мы используем в качестве базы:
Используя QFC в качестве основы, [latex] \ displaystyle \ frac {140} {75} = 1.867 \\ [/ latex].
Это говорит о том, что Albertsons на 186,7% больше, чем QFC.
Используя Альбертсона в качестве основы, [latex] \ displaystyle \ frac {140} {215} = 0.651 \ [/ латекс].
Это говорит о том, что QFC на 65,1% меньше, чем у Albertsons.
Обратите внимание, что оба они показывают процент различий . Мы также можем вычислить размер Альбертсона относительно QFC: [latex] \ displaystyle \ frac {215} {75} = 2.867 \\ [/ latex], что говорит нам, что размер Albertsons в 2,867 раз больше QFC. Точно так же мы могли бы вычислить размер QFC относительно Альбертсона: [latex] \ displaystyle \ frac {75} {215} = 0,349 \\ [/ latex], что говорит нам, что QFC составляет 34,9% от размера Albertsons.
Пример 7
Предположим, что акции упали в цене на 60% за одну неделю, а затем увеличились в стоимости на следующей неделе на 75%. Значение выше или ниже, чем было в начале?
Решение
Чтобы ответить на этот вопрос, предположим, что стоимость начинается с 100 долларов. Через неделю стоимость упала на 60%: 100 — 100 долларов (0,60) = 100 — 60 = 40 долларов.
Обратите внимание, что на следующей неделе основание процента изменилось на новое значение — 40 долларов. Расчет увеличения на 75%: 40 + 40 долларов (0.75) = 40 долларов + 30 долларов = 70 долларов.
В конце концов, акции все еще на 30 долларов ниже, или [latex] \ displaystyle \ frac {\ $ 30} {100} [/ latex] = 30% ниже, чем они были в начале.
Попробовать
Федеральный долг США в конце 2001 года составлял 5,77 триллиона долларов, а к концу 2002 года вырос до 6,20 триллиона долларов. В конце 2005 года он составлял 7,91 триллиона долларов, а к концу 2006 года вырос до 8,45 триллиона долларов. относительный рост за 2001–2002 гг. и 2005–2006 гг. В каком году федеральный долг увеличился больше?
Пример 8
В статье «Сиэтл Таймс» о количестве выпускников средних школ сообщается, что «количество школ, которые за четыре года заканчивают 60 процентов или меньше учащихся, иногда называемых« фабриками по выбыванию », уменьшилось на 17 за этот период.Число детей, посещающих школы с такими низкими показателями выпускников, сократилось вдвое ».
- Является ли «уменьшение на 17» полезным сравнением?
- Принимая во внимание последнее предложение, можем ли мы сделать вывод, что количество «фабрик, бросивших учебу» изначально составляло 34?
Раствор
- Это число трудно оценить, так как у нас нет оснований судить, большое это изменение или небольшое. Если количество «фабрик, бросающих учебу» упадет с 20 до 3, это будет очень существенное изменение, но если число упадет с 217 до 200, это будет меньшим улучшением.
- Последнее предложение обеспечивает относительное изменение, которое помогает увидеть первое предложение в перспективе. Мы можем оценить, что количество «фабрик, бросивших учебу», вероятно, ранее составляло около 34. Однако возможно, что ученики просто переместили школы, а не школа улучшилась, поэтому эта оценка может быть неточной.
Пример 9
В ходе дебатов на выборах вице-президента в 2004 году Эдвардс заявил, что американские войска понесли «90% потерь коалиции» в Ираке.Чейни оспорил это, заявив, что на самом деле иракские силы безопасности и союзники по коалиции «понесли почти 50 процентов» жертв. Кто прав?
Решение
Без дополнительной информации нам трудно судить, кто прав, но мы можем легко сделать вывод, что эти два процента говорят о разных вещах, поэтому одно не обязательно противоречит другому. Утверждение Эдварда было процентным соотношением с коалиционными силами в качестве основы процента, в то время как утверждение Чейни было процентным соотношением с коалиционными и иракскими силами безопасности в качестве основы процента.Оказывается, обе статистические данные довольно точны.
Попробовать
На президентских выборах 2012 года один кандидат утверждал, что «план президента сократит 716 миллиардов долларов из Medicare, что приведет к меньшему количеству услуг для пожилых людей», в то время как другой кандидат опровергает, что «наш план не сокращает текущие расходы, а фактически расширяет льготы для пожилых людей. , реализуя меры экономии ». Эти утверждения противоречат друг другу, согласуются или несопоставимы, потому что они говорят о разных вещах?
Завершим обзор процентов с несколькими предостережениями.Во-первых, когда мы говорим об изменении величин, которые уже измерены в процентах, мы должны быть осторожны в том, как мы описываем это изменение.
Пример 10
Поддержка политика увеличивается с 40% до 50% избирателей. Опишите изменение.
Решение
Мы могли бы описать это, используя абсолютное изменение: [латекс] | 50 \% — 40 \% | = 10 \% [/ latex]. Обратите внимание, что, поскольку исходные количества были процентами, это изменение также имеет единицы процента. В данном случае лучше всего описать это как увеличение на 10 процентных пунктов .
Напротив, мы можем вычислить процентное изменение: [latex] \ displaystyle \ frac {10 \%} {40 \%} = 0,25 = 25 \% [/ latex] увеличение. Это относительное изменение, и мы бы сказали, что поддержка политика увеличилась на 25%.
Наконец, предостережение от усреднения процентов.
Пример 11
Баскетболист забивает 40% попыток 2-х очковых бросков и 30% 3-х бросков с игры. Найдите общий процент бросков с игры.
Решение
Очень заманчиво усреднить эти значения и заявить, что общее среднее значение составляет 35%, но это, вероятно, неверно, так как большинство игроков делают гораздо больше 2-х очковых попыток, чем 3-х очковых.На самом деле у нас недостаточно информации, чтобы ответить на этот вопрос. Предположим, что игрок сделал 200 бросков с игры по 2 очка и 100 бросков с игры по 3 очка. Затем они сделали 200 (0,40) = 80 бросков по 2 очка и 100 (0,30) = 30 бросков по 3 очка. В целом они сделали 110 бросков из 300 при общем проценте бросков с игры [latex] \ displaystyle \ frac {110} {300} = 0,367 = 36,7 \% \ [/ latex].
Пропорции и нормы
Если бы вы хотели снабжать Сиэтл энергией ветра, сколько ветряных мельниц вам нужно было бы установить? На подобные вопросы можно ответить, используя ставки и пропорции.
Тарифы
Ставка — это соотношение (дробь) двух величин.
Ставка за единицу — это ставка со знаминателем, равным единице.
Пример 12
Ваша машина может проехать 300 миль на баке емкостью 15 галлонов. Выразите это как оценку.
Решение
Выражается как коэффициент [латекс] \ displaystyle \ frac {300 \ text {миль}} {15 \ text {галлонов}} \\ [/ latex]. Мы можем разделить, чтобы найти единицу измерения: [latex] \ displaystyle \ frac {20 \ text {miles}} {1 \ text {gallon}} \\ [/ latex], которую мы также можем записать как [latex] \ displaystyle {20} \ frac {\ text {miles}} {\ text {gallon}} \\ [/ latex], или всего 20 миль на галлон.
Уравнение пропорции
Уравнение пропорции — это уравнение, показывающее эквивалентность двух норм или соотношений.
Пример 13
Решите пропорцию [латекс] \ displaystyle \ frac {5} {3} = \ frac {x} {6} \\ [/ latex] для неизвестного значения x .
Решение
Эта пропорция просит нас найти дробь со знаминателем 6, которая эквивалентна дроби [latex] \ displaystyle \ frac {5} {3} \\ [/ latex]. Мы можем решить эту проблему, умножив обе части уравнения на 6, получив [latex] \ displaystyle {x} = \ frac {5} {3} \ cdot6 = 10 \\ [/ latex].
Пример 14
Масштаб карты показывает, что ½ дюйма на карте соответствует 3 реальным милям. На сколько миль друг от друга находятся два города, разделенных на карте [latex] \ displaystyle {2} \ frac {1} {4} \\ [/ latex] дюймами?
Решение
Мы можем установить пропорцию, установив равные два значения [latex] \ displaystyle \ frac {\ text {map дюймы}} {\ text {real miles}} \\ [/ latex] и введя переменную x , чтобы представить неизвестную величину — расстояние в миле между городами.
| [латекс] \ displaystyle \ frac {\ frac {1} {2} \ text {map inch}} {3 \ text {miles}} = \ frac {2 \ frac {1} {4} \ text {карта дюймов}} {x \ text {miles}} \\ [/ latex] | Умножаем обе стороны на x и переписываем смешанное число |
| [латекс] \ displaystyle \ frac {\ frac {1} {2}} {3} \ cdot {x} = \ frac {9} {4} \\ [/ latex] | Умножить обе стороны на 3 |
| [латекс] \ displaystyle \ frac {1} {2} x = \ frac {27} {4} \\ [/ latex] | Умножьте обе стороны на 2 (или разделите на ½) |
| [латекс] \ displaystyle {x} = \ frac {27} {2} = 13 \ frac {1} {2} \ text {miles} \\ [/ latex] |
Многие проблемы пропорций также могут быть решены с помощью анализа размеров , процесса умножения количества на нормы для изменения единиц.
Пример 15
Ваша машина может проехать 300 миль на баке емкостью 15 галлонов. Как далеко он может проехать на 40 галлонах?
Решение
Мы определенно могли бы ответить на этот вопрос, используя пропорцию: [латекс] \ displaystyle \ frac {300 \ text {miles}} {15 \ text {gallons}} = \ frac {x \ text {miles}} {40 \ text { галлонов}} \\ [/ латекс].
Однако ранее мы обнаружили, что 300 миль на 15 галлонах дают скорость 20 миль на галлон. Если мы умножим полученное количество 40 галлонов на этот коэффициент, галлона единицы «аннулируются», и у нас останется количество миль:
[латекс] \ displaystyle40 \ text {галлонов} \ cdot \ frac {20 \ text {миль}} {\ text {gallon}} = \ frac {40 \ text {галлонов}} {1} \ cdot \ frac {20 \ text {miles}} {\ text {gallons}} = 800 \ text {miles} \\ [/ latex]
Обратите внимание, если бы вместо этого нас спросили «сколько галлонов необходимо, чтобы проехать 50 миль?» мы могли бы ответить на этот вопрос, инвертировав скорость 20 миль на галлон так, чтобы блок миль аннулировал, и у нас остались галлоны:
[латекс] \ displaystyle {50} \ text {miles} \ cdot \ frac {1 \ text {gallon}} {20 \ text {miles}} = \ frac {50 \ text {miles}} {1} \ cdot \ frac {1 \ text {галлон}} {20 \ text {miles}} = \ frac {50 \ text {gallons}} {20} = 2.5 \ text {галлонов} \\ [/ latex]
Размерный анализ также можно использовать для преобразования единиц измерения. Вот несколько единиц преобразования для справки.
Преобразование единиц
Длина
| 1 фут (фут) = 12 дюймов (дюймов) | 1 ярд (ярд) = 3 фута (фут) |
| 1 миля = 5280 футов | |
| 1000 миллиметров (мм) = 1 метр (м) | 100 сантиметров (см) = 1 метр |
| 1000 метров (м) = 1 километр (км) | 2.54 сантиметра (см) = 1 дюйм |
Масса и масса
| 1 фунт (фунт) = 16 унций (унций) | 1 тонна = 2000 фунтов |
| 1000 миллиграммов (мг) = 1 грамм (г) | 1000 грамм = 1 килограмм (кг) |
| 1 килограмм = 2,2 фунта (на Земле) |
Вместимость
| 1 чашка = 8 жидких унций (жидких унций) | 1 пинта = 2 чашки |
| 1 кварта = 2 пинты = 4 чашки | 1 галлон = 4 кварты = 16 чашек |
| 1000 миллилитров (мл) = 1 литр (л) |
Пример 16
Велосипед движется со скоростью 15 миль в час.Сколько футов он преодолеет за 20 секунд?
Решение
Чтобы ответить на этот вопрос, нам нужно преобразовать 20 секунд в футы. Если бы мы знали скорость велосипеда в футах в секунду, этот вопрос был бы проще. Поскольку мы этого не делаем, нам нужно будет выполнить дополнительные преобразования единиц. Нам нужно знать, что 5280 футов = 1 миля. Мы могли бы начать с преобразования 20 секунд в часы:
[латекс] \ displaystyle {20} \ text {секунды} \ cdot \ frac {1 \ text {минута}} {60 \ text {секунды}} \ cdot \ frac {1 \ text {час}} {60 \ text {minutes}} = \ frac {1} {180} \ text {hour} \\ [/ latex]
Теперь мы можем умножить на 15 миль / час
[латекс] \ displaystyle \ frac {1} {180} \ text {hour} \ cdot \ frac {15 \ text {miles}} {1 \ text {hour}} = \ frac {1} {12} \ text {mile} \\ [/ latex]
Теперь мы можем преобразовать в футы
[латекс] \ displaystyle \ frac {1} {12} \ text {mile} \ cdot \ frac {5280 \ text {feet}} {1 \ text {mile}} = 440 \ text {ft} \\ [/ латекс]
Мы могли бы также провести весь этот расчет в одном длинном наборе продуктов:
[латекс] \ displaystyle20 \ text {секунды} \ cdot \ frac {1 \ text {минута}} {60 \ text {секунды}} \ cdot \ frac {1 \ text {час}} {60 \ text {минуты} } = \ frac {15 \ text {miles}} {1 \ text {miles}} = \ frac {5280 \ text {ft}} {1 \ text {mile}} = \ frac {1} {180} \ text {час} \\ [/ латекс]
Попробовать
Катушка длиной 1000 футов с голым медным проводом 12-го калибра весит 19.8 фунтов. Сколько будет весить 18 дюймов проволоки в унциях?
Обратите внимание, что в примере миль на галлон, если мы удваиваем пройденные мили, мы удваиваем расход топлива. Аналогично, в примере с расстоянием на карте, если расстояние на карте удваивается, реальное расстояние удваивается. Это ключевая особенность пропорциональных отношений, которую мы должны подтвердить, прежде чем предполагать, что две вещи связаны пропорционально.
Пример 17
Предположим, вы кладете плитку на пол в комнате размером 10 на 10 футов и обнаруживаете, что вам потребуется 100 плиток.2} \\ [/ latex]
Другие величины просто не масштабируются пропорционально.
Пример 18
Предположим, небольшая компания тратит 1000 долларов на рекламную кампанию и получает от нее 100 новых клиентов. Сколько новых клиентов им следует ожидать, если они потратят 10 000 долларов?
Решение
Хотя соблазнительно сказать, что они получат 1000 новых клиентов, вполне вероятно, что дополнительная реклама будет менее эффективной, чем первоначальная. Например, если компания представляет собой магазин джакузи, скорее всего, только определенное количество людей заинтересовано в покупке джакузи, поэтому в городе может не быть даже 1000 человек, которые были бы потенциальными покупателями.
Иногда при работе с ставками, пропорциями и процентами процесс может быть усложнен величиной задействованных чисел. Иногда большие числа просто трудно понять.
Пример 19
Сравните военный бюджет США на 2010 год в размере 683,7 миллиарда долларов с другими величинами.
Решение
Здесь выписано очень большое число, около 683 700 000 000 долларов. Конечно, вообразить миллиард долларов очень сложно, поэтому можно сравнить его с другими величинами.
Если бы эта сумма была использована для выплаты заработной платы 1,4 миллиона сотрудников Walmart в США, каждый заработал бы более 488000 долларов.
В США проживает около 300 миллионов человек. Военный бюджет составляет около 2200 долларов на человека.
Если вы вложите 683,7 миллиарда долларов в 100-долларовые банкноты и отсчитываете 1 в секунду, то на завершение счета потребуется 216 лет.
Пример 20
Сравните потребление электроэнергии на душу населения в Китае и Японии.
Решение
Чтобы ответить на этот вопрос, нам сначала потребуются данные. На веб-сайте ЦРУ мы можем узнать, что потребление электроэнергии в Китае в 2011 году составило 4 693 000 000 000 кВтч (киловатт-часов), или 4,693 триллиона кВтч, в то время как потребление в Японии составило 859 700 000 000 или 859,7 миллиарда кВтч. Чтобы найти показатель на душу населения (на человека), нам также понадобится население двух стран. По данным Всемирного банка, население Китая составляет 1 344 130 000 человек, или 1,344 миллиарда человек, а население Японии — 127 817 277 человек, или 127 человек.8 миллионов.
Расчет потребления на душу населения для каждой страны:
Китай: [латекс] \ displaystyle \ frac {4,693,000,000,000 \ text {KWH}} {1,344,130,000 \ text {people}} \\ [/ latex] ≈ 3491,5 кВтч на человека
Япония: [латекс] \ displaystyle \ frac {859,700,000,000 \ text {KWH}} {127 817 277 \ text {people}} \\ [/ latex] ≈ 6726 кВт / ч на человека
В то время как Китай в целом потребляет более чем в 5 раз больше электроэнергии, чем Япония, из-за того, что население Японии намного меньше, оказывается, что Япония потребляет почти вдвое больше электроэнергии на человека по сравнению с Китаем.
Геометрия
Геометрические формы, а также площадь и объемы часто могут иметь важное значение при решении проблем.
Пример 21
Вам интересно, насколько высокое дерево, но у вас нет возможности взобраться на него. Опишите метод определения высоты.
Решение
Есть несколько подходов, которые мы могли бы использовать. Мы воспользуемся одним, основанным на треугольниках, что требует наличия солнечного дня. Предположим, что дерево отбрасывает тень, скажем, 15 футов в длину. Затем я могу попросить друга помочь мне измерить мою собственную тень.Предположим, я ростом 6 футов и отбрасываю тень 1,5 фута. Поскольку треугольник, образованный деревом и его тенью, имеет те же углы, что и треугольник, образованный мной и моей тенью, эти треугольники называются аналогичными треугольниками , и их стороны будут пропорционально масштабироваться. Другими словами, отношение высоты к ширине будет одинаковым в обоих треугольниках. Используя это, мы можем найти высоту дерева, которую мы обозначим как h :
.
[латекс] \ displaystyle \ frac {6 \ text {ft tall}} {1,5 \ text {ft shadow}} = \ frac {h \ text {ft tall}} {15 \ text {ft shadow}} \\ [ / латекс]
Умножая обе части на 15, получаем h = 60.Дерево около 60 футов высотой.
Может быть полезно вспомнить некоторые формулы для площадей и объемов нескольких основных форм.
Площади
Прямоугольник
Площадь: Д · З
Периметр: 2 L + 2 W
Круг
Радиус: r
Площадь: π r 2
Окружность: 2π r
Объемы
Прямоугольная коробка
Объем: Д · Ш · В
Цилиндр
Объем: π r 2 H
Пример 22
Если для пиццы диаметром 12 дюймов требуется 10 унций теста, сколько теста необходимо для пиццы диаметром 16 дюймов?
Решение
Чтобы ответить на этот вопрос, нам нужно рассмотреть, как вес теста будет изменяться.2} \\ [/ latex]
Умножить обе стороны на 201
[латекс] \ displaystyle {x} = 201 \ cdot \ frac {10} {113} \\ [/ latex] = около 17,8 унций теста для пиццы размером 16 дюймов.
Интересно отметить, что хотя диаметр [латекс] \ displaystyle \ frac {16} {12} \\ [/ latex] = в 1,33 раза больше, требуемое тесто, которое масштабируется с площадью, составляет 1,33 2 = В 1,78 раза больше.
Пример 23
Компания производит зефир обыкновенный и джамбо. Обычный зефир содержит 25 калорий.Сколько калорий будет в огромном зефире?
Решение
Мы ожидаем, что количество калорий будет увеличиваться с увеличением объема. Поскольку зефир имеет цилиндрическую форму, мы можем использовать эту формулу для определения объема. По сетке на изображении мы можем оценить радиус и высоту каждого зефира.
Обычный зефир имеет диаметр около 3,5 единиц, что дает радиус 1,75 единицы и высоту около 3,5 единиц. Объем примерно равен π (1,75) 2 (3.3} = 88,1 \ text {калории} \\ [/ latex]
Интересно отметить, что хотя диаметр и высота зефира примерно в 1,5 раза больше, объем и калорийность примерно в 1,5 3 = 3,375 раза больше.
Попробовать
На веб-сайте говорится, что вам понадобится 48 мешков по 50 фунтов с песком, чтобы заполнить песочницу размером 8 футов на 8 футов на 1 фут. Сколько мешков вам понадобится для песочницы размером 6 на 4 на 1 фут?
Решение проблем и оценка
Наконец, мы соберем изученные математические инструменты и воспользуемся ими для решения более сложных задач.Во многих задачах возникает соблазн взять данную информацию, вставить ее в любые формулы, которые у вас есть под рукой, и надеяться, что результат будет тем, что вы должны были найти. Скорее всего, этот подход хорошо послужил вам в других математических классах.
Этот подход не подходит для реальных жизненных проблем. Вместо этого к решению проблем лучше всего начинать с конца: точно определить, что вы ищете. Затем вы работаете в обратном направлении, спрашивая «какая информация и процедуры мне понадобятся, чтобы найти это?» На очень мало интересных вопросов можно ответить за один математический шаг; часто вам нужно будет связать воедино путь решения, серию шагов, которые позволят вам ответить на вопрос.
Процесс решения проблем
- Определите вопрос, на который вы пытаетесь ответить.
- Работайте в обратном направлении, определяя информацию, которая вам понадобится, и отношения, которые вы будете использовать, чтобы ответить на этот вопрос.
- Продолжайте работать в обратном направлении, создавая путь решения.
- Если вам не хватает необходимой информации, найдите ее или оцените. Если у вас есть ненужная информация, игнорируйте ее.
- Решите проблему, следуя своему пути решения.
В большинстве задач, с которыми мы работаем, мы будем приближать решение, потому что у нас не будет точной информации. Мы начнем с нескольких примеров, на которых мы сможем приблизить решение, используя базовые знания из нашей жизни.
Пример 24
Сколько раз в год бьется ваше сердце?
Решение
Этот вопрос задает частоту сердечных сокращений за год. Поскольку год — большой срок для измерения сердечных сокращений, если бы мы знали частоту сердечных сокращений в минуту, мы могли бы масштабировать это количество до года.Итак, информация, которая нам нужна, чтобы ответить на этот вопрос, — это число ударов сердца в минуту. Это то, что вы можете легко измерить, посчитав свой пульс, глядя на часы в течение минуты.
Предположим, вы считаете 80 ударов в минуту. Чтобы преобразовать количество ударов в год:
[латекс] \ displaystyle \ frac {80 \ text {beats}} {1 \ text {minute}} \ cdot \ frac {60 \ text {minutes}} {1 \ text {hour}} \ cdot \ frac {24 \ text {часы}} {1 \ text {день}} \ cdot \ frac {365 \ text {days}} {1 \ text {год}} = 42 048 000 \ text {ударов в год} \\ [/ latex]
Пример 25
Какой толщины у одного листа бумаги? Сколько это весит?
Решение
Хотя у вас может быть под рукой лист бумаги, попытаться измерить его будет непросто.Вместо этого мы могли бы представить стопку бумаги, а затем масштабировать толщину и вес до одного листа. Если вы когда-нибудь покупали бумагу для принтера или копировального аппарата, вы, вероятно, купили стопку бумаги, в которой содержится 500 листов. По нашим оценкам, пачка бумаги имеет толщину около 2 дюймов и весит около 5 фунтов. Уменьшение масштаба,
[латекс] \ displaystyle \ frac {2 \ text {дюймы}} {\ text {ream}} \ cdot \ frac {1 \ text {ream}} {500 \ text {pages}} = 0,004 \ text {дюймов на лист} \\ [/ латекс]
[латекс] \ displaystyle \ frac {5 \ text {pounds}} {\ text {ream}} \ cdot \ frac {1 \ text {ream}} {500 \ text {pages}} = 0.01 \ text {фунтов на лист, или} = 0,16 \ text {унций на лист.} \\ [/ latex]
Пример 26
Рецепт маффинов из цуккини гласит, что из него получается 12 маффинов с 250 калориями на каждый маффин. Вместо этого вы решаете приготовить мини-кексы, и по рецепту получается 20 кексов. Если вы съедите 4, сколько калорий вы потребляете?
Решение
Есть несколько возможных путей решения этого вопроса. Мы рассмотрим один.
Чтобы ответить на вопрос о том, сколько калорий будут содержать 4 мини-маффина, нам нужно знать количество калорий в каждом мини-маффине.Чтобы узнать количество калорий в каждом мини-маффине, мы могли бы сначала найти общее количество калорий для всего рецепта, а затем разделить его на количество произведенных мини-маффинов. Чтобы найти общее количество калорий для рецепта, мы могли бы умножить количество калорий в стандартном маффине на их количество. Обратите внимание, что это дает многоэтапный путь решения. Часто проще решить проблему небольшими шагами, чем пытаться найти способ сразу перейти от данной информации к решению.
Теперь мы можем выполнить наш план:
[латекс] \ displaystyle {12} \ text {маффины} \ cdot \ frac {250 \ text {калории}} {\ text {muffin}} = 3000 \ text {калорий на весь рецепт} \\ [/ latex]
[латекс] \ displaystyle \ frac {3000 \ text {калории}} {20 \ text {мини-маффины}} = \ text {дает} 150 \ text {калорий на мини-маффин} \\ [/ latex]
[латекс] \ displaystyle4 \ text {мини-маффины} \ cdot \ frac {150 \ text {калории}} {\ text {mini-muffin}} = \ text {totals} 600 \ text {израсходовано калорий.} \\ [/ latex]
Пример 27
Вам нужно заменить доски в колоде. Примерно сколько будут стоить материалы?
Решение
Есть два подхода, которые мы могли бы применить к этой проблеме: 1) оценить количество досок, которые нам понадобятся, и определить стоимость доски, или 2) оценить площадь настила и найти приблизительную стоимость квадратного фута для досок настила. Мы воспользуемся вторым подходом.
Для этого пути решения мы сможем ответить на вопрос, знаем ли мы стоимость квадратного фута террасных досок и квадратные метры террасы.Чтобы найти стоимость квадратного фута для террасной доски, мы могли бы вычислить площадь одной доски и разделить ее на стоимость этой доски. Мы можем вычислить квадратные метры настила, используя геометрические формулы. Итак, сначала нам нужна информация: размеры колоды, а также стоимость и размеры одинарной террасной доски.
Предположим, что палуба имеет прямоугольную форму размером 16 на 24 фута и имеет общую площадь 384 фута. 2 .
Посетив местный домашний магазин, вы обнаружили, что кедровая доска размером 8 на 4 дюйма стоит около 7 долларов.2} = \ 1080 $ \ text {общая стоимость} \\ [/ latex]
Конечно, эта смета расходов предполагает отсутствие отходов, что случается редко. Обычно для учета отходов к смете затрат добавляют не менее 10%.
Пример 28
Стоит ли покупать гибрид Hyundai Sonata вместо обычной Hyundai Sonata?
Решение
Чтобы принять это решение, мы должны сначала решить, что будет нашей базой для сравнения. В этом примере мы сосредоточимся на расходах на топливо и закупку, но покупатель может принять во внимание влияние на окружающую среду и затраты на техническое обслуживание.
Было бы интересно сравнить стоимость бензина для работы обеих машин в течение года. Чтобы определить это, нам нужно знать, сколько миль на галлон получают обе машины, а также сколько миль мы планируем проехать за год. Из этой информации мы можем найти необходимое количество галлонов в год. Используя цену на газ за галлон, мы можем найти текущие расходы.
По данным веб-сайта Hyundai, Sonata 2013 будет иметь скорость 24 мили на галлон (миль на галлон) в городе и 35 миль на галлон на шоссе.Гибрид получит 35 миль на галлон в городе и 40 миль на галлон на шоссе.
Средний водитель проезжает около 12 000 миль в год. Предположим, вы планируете проезжать около 75% этого количества в городе, то есть 9 000 городских миль в год и 3 000 миль по шоссе в год.
Затем мы можем найти количество галлонов, которое потребуется каждой машине в течение года.
Соната: [латекс] \ displaystyle {9000} \ text {городские мили} \ cdot \ frac {1 \ text {галлон}} {24 \ text {городские мили}} + 3000 \ text {шоссе миль} \ cdot \ frac {1 \ text {галлон}} {35 \ text {шоссе миль}} = 460.7 \ text {gallons} [/ latex]
Гибрид: [латекс] \ displaystyle {9000} \ text {городские мили} \ cdot \ frac {1 \ text {галлон}} {35 \ text {городские мили}} + 3000 \ text {шоссе миль} \ cdot \ frac {1 \ text {галлон}} {40 \ text {шоссе миль}} = 332,1 \ text {галлон} [/ latex]
Если газ в вашем районе в среднем стоит около 3,50 долларов за галлон, мы можем использовать это, чтобы определить текущие расходы:
Соната: [латекс] \ displaystyle {460.7} \ text {галлонов} \ cdot \ frac {\ $ 3.50} {\ text {gallon}} = \ $ 1612.45 \\ [/ latex]
Гибрид: [латекс] \ displaystyle {332.1} \ text {галлонов} \ cdot \ frac {\ $ 3.50} {\ text {галлон}} = \ $ 1162.35 \\ [/ latex]
Гибрид сэкономит 450,10 долларов в год. Затраты на бензин для гибрида примерно [latex] \ displaystyle \ frac {\ $ 450.10} {\ $ 1612.45} \\ [/ latex] = 0,279 = 27,9% ниже, чем затраты на стандартную Sonata.
Хотя здесь полезны как абсолютные, так и относительные сравнения, они все же затрудняют ответ на исходный вопрос, поскольку «стоит ли оно того» подразумевает некоторый компромисс для экономии газа. Действительно, гибридная Sonata стоит около 25 850 долларов, по сравнению с базовой моделью для обычной Sonata — 20 895 долларов.
Чтобы лучше ответить на вопрос «стоит ли оно того», мы могли бы изучить, сколько времени потребуется экономии газа, чтобы компенсировать дополнительные начальные затраты. Гибрид стоит на 4965 долларов дороже. При экономии газа в размере 451,10 доллара в год потребуется около 11 лет, чтобы экономия на газе окупила более высокие первоначальные затраты.
Можно сделать вывод, что если вы рассчитываете владеть автомобилем 11 лет, гибрид действительно того стоит. Если вы планируете владеть автомобилем менее 11 лет, возможно, оно того стоит, поскольку стоимость гибрида при перепродаже может быть выше или по другим причинам, не связанным с деньгами.Это тот случай, когда математика может помочь вам принять решение, но не может сделать его за вас.
Попробовать
Если вы путешествуете из Сиэтла, штат Вашингтон, в Спокан, штат Вашингтон, на трехдневную конференцию, имеет ли смысл водить или летать?
Решили? Вы умнее десятилетнего сингапурца? | Математика
Сегодня я задал вам десять вопросов с Международного конкурса математиков в Сингапуре в этом году. Вот вопросы и ответы. В целом у вас все получилось — умнее 10-летнего сингапурца! (С оговоркой, что у них не было ответов с несколькими вариантами ответов на выбор, а их всего десять).Единственные вопросы, на которые ваш самый популярный ответ неправильный, — это 6 и 8. (C в Q6 и B в Q8). Спасибо за участие — теперь просмотрите свои наработки …
Для учеников 5 класса:
1. Мэри отрезала 2/5 веревки. Позже она отрезала еще 14 м. Отношение длины оставшейся струны к общей отрезанной длине составляет 1: 3. Какова длина оставшейся струны?
- A. 5 м
- Б. 7 м
- С.10 м
- Д. 14 м
Решение — C. [73 процента читателей правильно поняли]
О, Мэри! Вот как я бы решил это, используя уравнения. Пусть L будет исходной длиной строки, а R будет тем, что останется после того, как вы дважды разрежете строку. Мы знаем, что R = (L x 3/5) — 14m, и что ((L x 2/5) +14) / R = 3, или 2L / 5 + 14 = 3R. Подставляя первое уравнение во второе, получаем 2L / 5 + 14 = 9L / 5 –42. Что меняется на: 7L / 5 = 56 или L = 40.Итак, R = 10м.
Интересно, что сингапурский метод решения другой. Это требует от нас более визуального восприятия строки: мы разрезаем ее на 2/5. Затем 14 м, и остается кусок, размер которого составляет треть от того, что было вырезано. Другими словами, у нас остается 1/4 исходной длины. Чтобы сравнить дроби 2/5, а затем 1/4, давайте изменим их на наименьший общий знаменатель, равный 20. Итак, мы отсекаем 8/20, вычитаем 14m и получаем 5/20. Давайте теперь нарисуем струну, разделенную на двадцатые части:
14 метров должны составлять 7/20 длины, что означает, что каждая двадцатая часть равна 2 метрам.Оставшийся кусок веревки равен 5/20, т.е. 10 м
2. Площади граней прямоугольной коробки составляют 84 см 2 , 70 см 2 и 30 см 2 . Какой объем коробки?
Фотография: ISMC
- A. 300 см 3
- Б. 420 см 3
- C. 490 см 3
- Д. 504 см 3
Решение — B . [85 процентов читателей правильно поняли]
Сначала нам нужно определить возможные длины сторон, посмотрев, какие два числа умножаются на площадь каждой грани.Грань 84 может быть 1 x 84, 2 x 42, 3 x 28, 4 x 21, 6 x 14 или 7 x 12. Грань 70 может быть 1 x 70, 2 x 35, 5 x 14 или 7 x 10. Грань 30 может быть 1 x 30, 2 x 15, 3 x 10 или 5 x 6.
- Общие множители между 84 и 70 равны 1, 2, 7 и 14.
- Общие множители между 84 и 30 равны 1, 2, 3 и 6.
Единственный способ получить 84 с каждым из этих общих множителей — это 14 от верхней строки и 6 снизу. Таким образом, край, граничащий с гранями 84 и 70, имеет длину 14, а край, ограничивающий края 84 и 30, имеет длину 6.Это означает, что высота должна быть 30/6, или 70/14 = 5. Таким образом, объем 14 x 6 x 5 = 420 см.
3. Всего четыре числа. Если пропустить какое-либо одно число, среднее значение оставшихся трех чисел будет 45, 60, 65 или 70. Какое среднее значение всех четырех чисел?
Решение — C . [82 процента читателей правильно поняли]
Если четыре числа — A, B, C и D, то мы знаем, что
- A + B + C = 45 × 3
- A + B + D = 60 × 3
- A + C + D = 65 × 3
- B + C + D = 70 × 3
Теперь сложите их, чтобы получить 3 A + 3 B + 3 C + 3 D = (45 + 60 + 65 + 70) × 3
Это A + B + C + D = (45 + 60 + 65 + 70) = 240 . Таким образом, их среднее значение составляет 240/4 = 60
4. Марш проходит по улицам от школы (S) до общественного центра (CC). Одна из улиц закрыта. Если марш может идти только на восток или юг, каково количество различных способов добраться до общественного центра? [10 процентов]
Фотография: ISMC
Решение — B. [46 процентов читателей правильно поняли]
Есть 19 возможных способов:
5. Салли дали набор из 5 карточек, пронумерованных от 1 до 5. Петру также дали набор из 5 карточек с номерами от 1 до 5.Затем им завязали глаза и попросили выбрать карту из своих наборов. Сумма чисел на двух карточках была сообщена только Салли, а произведение чисел — только Питеру. Затем им было предложено угадать два числа. Вот что сказал каждый из них:
Питер: Я не знаю двух чисел.
Салли: Теперь я знаю два числа.
Питер: Я до сих пор не знаю двух чисел.
Салли: Позвольте помочь вам.Число, которое мне сказали, больше, чем вам сказали.
Питер: Теперь я знаю два числа.
Какие два числа?
- A. 1 и 4
- Б. 1 и 5
- C. 2 и 4
- Д. 2 и 5
Решение: A. [72 процента читателей правильно поняли]
Поскольку каждому из них были даны числа от 1 до 5, если бы Питеру сказали любое из следующих чисел, он мог бы сказать, что это за были выбраны два числа:
- 1 → 1 × 1 Два числа — 1 и 1.
- 2 → 1 × 2 Два числа — 1 и 2.
- 3 → 1 × 3 Два числа — 1 и 3.
- 5 → 1 × 5 Два числа — 1 и 5.
- 6 → 2 × 3 Два числа — 2 и 3.
- 7 → 1 × 7 Два числа — 1 и 7.
- 8 → 2 × 4 Два числа — 2 и 4.
- 9 → 3 × 3 Две цифры — 3 и 3.
- 10 → 2 × 5 Два числа — 2 и 5.
- 12 → 3 × 4 Две цифры — 3 и 4.
- 15 → 3 × 5 Две цифры — 3 и 5.
- 16 → 4 × 4 Два числа — 4 и 4.
- 20 → 4 × 5 Два числа — 4 и 5.
- 25 → 5 × 5 Две цифры — 5 и 5.
(Продукты 11, 13, 14, 17, 18, 19, 21, 22, 23 и 24 не могут быть сформированы.)
Единственное неоднозначное произведение — 4, поскольку 4 может быть равно 1 × 4 или 2 × 2. Таким образом, когда Питер сказал, что он не знает чисел, Салли сможет узнать, что произведение, которое, по словам Питера, должно быть 4.Поскольку Салли сказала, что сумма, которую ей сказали, больше, чем произведение, которое было сказано Питеру, , два числа, которые были выбраны, должны были быть 1 и 4 (сумма = 5), а не 2 и 2 (сумма = 4).
Для учеников 6 класса:
6. Имеется 4 ключа и 4 замка. Какое максимальное количество раз вам нужно попробовать замки, чтобы все 4 ключа совпали с их замками?
Решение — B. [30 процентов читателей правильно поняли]
Если вы попробуете 3 ключа на замке 1 st , вы узнаете, что 4 -й ключ совпадает.Итак, вам нужно максимум 3 попытки. Точно так же для блокировки 2 nd требуется максимум 2 попытки, а для блокировки 3 rd требуется только 1 попытка. Таким образом, необходимо 3 + 2 + 1 = 6 попыток.
7. На диаграмме (не в масштабе) наклонная линия делит площадь прямоугольника в соотношении 1: 6. Каково соотношение a : b ?
Фотография: ISMC
- A. 2: 3
- Б. 1: 2
- С. 2: 5
- Д.1: 3
Решение — C. [63 процента читателей правильно поняли]
Верхний прямоугольник имеет площадь 2 единицы 2 , нижний прямоугольник имеет площадь 6 — 1 = 5 единиц 2 . Мы знаем, что отношение площади верхнего прямоугольника к площади нижнего прямоугольника равно 2: 5. Поскольку оба прямоугольника имеют одинаковую ширину, то a и b также должны быть в соотношении 2: 5.
8. Сколько раз часовая и минутная стрелки часов образуют прямой угол друг с другом между 06:00 и 12:00 в один и тот же день?
Решение: A. [39 процентов читателей правильно поняли]
Время, когда часовая и минутная стрелки часов образуют прямой угол друг с другом в период с 06:00 до 12:00, составляет примерно 0617, 0649, 0722, 0754, 0828, 0900. , 0933, 1005, 1038, 1111, 1149.
Обратите внимание, что это происходит дважды в час, за исключением периода между 0800 и 1000, когда это происходит только три раза, а не четыре раза, как ожидалось. Это потому, что в 09:00 стрелки образуют прямой угол. Таким образом, с 06:00 до 12:00 это происходит (6 × 2) — 1 = 11 раз.
9. В школе 6 учеников 240 человек. Отношение количества студентов, которым нравится наука, к количеству студентов, которые не любят математику, составляет 5: 3. Отношение количества студентов, которым нравится математика, к количеству студентов, которые не любят, составляет 7: 5. Количество студентов, которым нравится и наука. и математике — 86. Сколько студентов не любят и естественные науки, и математику?
Решение , номер B . [75 процентов читателей правильно поняли]
Лучший способ решить эту проблему — использовать диаграмму Венна:
Теперь мы можем записать некоторые суммы:
Если количество студентов, которые любят науку, разделить на количество студентов, которые этого не делают, — 5/3, затем 5/8 от общего числа любят естественные науки, а 3/8 — нет.Поскольку общее количество студентов составляет 240, то число тех, кто любит науку, равно (5/8) x 240 = 150
Таким образом, количество студентов, которым нравится только , наука = 150 — 86 = 64
Аналогично числу студентов, которым нравится математика = (7/12) x 240 = 140
Итак, количество студентов, которым нравится только , математика = 140 — 86 = 54
Таким образом, количество студентов, которым не нравятся и естественные науки, и математика, составляет 240 — (64 + 86 + 54) = 36
10.У моего учителя было 3 больших коробки конфет. В каждой коробке лежали конфеты разного цвета. Каждому ученику раздали по 5 конфет двух разных цветов. Если каждый ученик в классе получил разную комбинацию цветов, каково было наибольшее возможное количество учеников в классе?
Решение — B. [67 процентов читателей правильно поняли]
Предположим, что это три цвета: красный, синий и желтый. Для любых двух цветов существует всего 4 различных комбинации. Итак, для красного и синего комбинации следующие:
- R R R R B
- Р Р Р Б Б
- R R B B B
- R B B B B
Есть 3 способа выбрать 2 цвета из 3:
- красно-синий,
- желто-голубой
- красно-желтый
Итак, разные цветовые комбинации для 5 конфет составляют 4 × 3 = 12 комбинаций.Следовательно, максимально возможное количество учеников — 12.
Надеюсь, вам понравились эти головоломки. Я вернусь с еще несколькими тизерами через две недели.
Спасибо Рою Ло из Международного конкурса математиков в Сингапуре.
